题目内容
函数 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A. | B. | C. | D. |
B.
解析试题分析:函数 在
在 上是连续函数,由于
上是连续函数,由于 ,
, ,所以
,所以 ,根据零点存在性定理可得零点所在的大致区间为
,根据零点存在性定理可得零点所在的大致区间为 .
.
考点:函数零点的判定定理.

练习册系列答案
相关题目
设二次函数 在区间[0,1]上单调递减,且
在区间[0,1]上单调递减,且 ,则实数
,则实数 的取值范围是( ).
的取值范围是( ).
| A.(-∞,0] | B.[2,+∞) | C.[0,2] | D.(-∞,0]∪[2,+∞) |
已知函数 ,则
,则 ( )
( )
A. | B. | C.1 | D.7 |
若函数 ,则
,则 (其中
(其中 为自然对数的底数)( )
为自然对数的底数)( )
A. | B. | C. | D. |
已知实数 满足
满足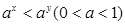 ,则下列关系式恒成立的是( )
,则下列关系式恒成立的是( )
A. | B. |
C.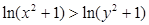 | D. |
 的两条切线PM、PN,切点分
的两条切线PM、PN,切点分 别为M、N.
别为M、N. 时,求函数
时,求函数 的单调
的单调 递增区间;
递增区间; ,试求函数
,试求函数 ,在区间
,在区间 内,总存在m+1个数
内,总存在m+1个数 使得不等式
使得不等式 成立,求m的最大值.
成立,求m的最大值. 、
、 满足
满足 ,则称
,则称 上的一组正交函数,给出三组函数:①
上的一组正交函数,给出三组函数:① ;②
;② ;③
;③ .
. 的图象可能是( )
的图象可能是( )