题目内容
（本小题满分12分）
已知
，
．
（1）求
的单调区间；
（2）若
时，
恒成立，求实数
的取值范围；
（3）当
时，证明：
．
（1）①
时，
在
上单调递减；
②
时，
，单调增区间为
，单调减区间为
；
③
时，
，单调增区间为
，单调减区间为
．
（2）
（3）证明见解析。
解析:
（1）
…………………………1分
当
，即
时，
，所以在上单调递减……………2分
当
，即
时，
①
时，，单调增区间为，单调减区间为……………3分
②时，，单调增区间为，单调减区间为………5分
综上：①时，在上单调递减（只要写出以上
三种情况即得5分）
②时，，单调增区间为，单调减区间为
③时，，单调增区间为，单调减区间为
（2）
恒成立，等价于
…………………………6分
，
，
在
上单调递减，
，
在上单调递减，
所以的最大值为
，所以…………………………8分
（3）证法一：由（2）知当
时，时，
恒成立
所以时，有
…………………………10分
所以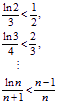
相乘得…………………………12分
方法二：数学归纳法
①当
时，显然成立…………………9分
②假设
（）成立，即
那么当
时，
下面只需证
，
设
，所以设
由（2）知当时，时，恒成立，
即
在恒成立，所以
综合①②命题成立…………………………………………………………12
分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
