题目内容
对n∈N*,不等式组
所表示的平面区域为Dn,Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列.(x1,y1)(x2,y2),(x3,y3),…,(xn,yn)
(1)求xn,yn;
(2)数列{an}满足a1=x1,且n≥2时an=
(
+
+…+
).证明当n≥2时,
-
=
;
|
(1)求xn,yn;
(2)数列{an}满足a1=x1,且n≥2时an=
| y | 2 n |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| an+1 |
| (n+1) |
| an |
| n2 |
| 1 |
| n2 |
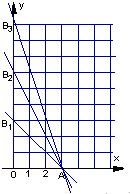
分析:(1)-nx+2n>0⇒x<2,x=1.故Dn内的整点都落在直线x=1上,且y≤n,故Dn内的整点按其到原点的距离从近到远排成的点列为(1,1),(1,2),…,(1,n),故xn=1,yn=n.
(2)证明:当n≥2时,由an= yn2 (
+
+…+
),,得
=
+
+…+
,再由错位相减法可知当n≥2时,
-
=
.
(2)证明:当n≥2时,由an= yn2 (
| 1 |
| y12 |
| 1 |
| y22 |
| 1 |
| yn-12 |
| an |
| yn2 |
| 1 |
| y12 |
| 1 |
| y22 |
| 1 |
| yn-12 |
| an+1 |
| (n+1) |
| an |
| n2 |
| 1 |
| n2 |
解答:解:(1)-nx+2n>0⇒x<2,∵x>0,且x∈N*,∴x=1.
故Dn内的整点都落在直线x=1上,且y≤n,
故Dn内的整点按其到原点的距离从近到远排成的点列为(1,1),(1,2),…,(1,n),
∴xn=1,yn=n.
(2)证明:当n≥2时,
由an= yn2 (
+
+…+
),
得
=
+
+…+
,
即
=
+
+…+
…①
∴
=
+
+…+
…②
②式减①式,得
-
=
.
故Dn内的整点都落在直线x=1上,且y≤n,
故Dn内的整点按其到原点的距离从近到远排成的点列为(1,1),(1,2),…,(1,n),
∴xn=1,yn=n.
(2)证明:当n≥2时,
由an= yn2 (
| 1 |
| y12 |
| 1 |
| y22 |
| 1 |
| yn-12 |
得
| an |
| yn2 |
| 1 |
| y12 |
| 1 |
| y22 |
| 1 |
| yn-12 |
即
| an |
| n2 |
| 1 |
| 12 |
| 1 |
| 22 |
| 1 |
| (n-1)2 |
∴
| an+1 |
| (n+1)2 |
| 1 |
| 12 |
| 1 |
| 22 |
| 1 |
| n2 |
②式减①式,得
| an+1 |
| (n+1)2 |
| an |
| n2 |
| 1 |
| n2 |
点评:本题考查数列和不等式的综合应用,解题时要认真审题,注意挖掘题设中的隐含条件,注意公式的灵活运用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 在平面直角坐标系上,设不等式组
在平面直角坐标系上,设不等式组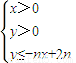 所表示的平面区域为Dn,Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列.(x1,y1)(x2,y2),(x3,y3),…,(xn,yn)
所表示的平面区域为Dn,Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列.(x1,y1)(x2,y2),(x3,y3),…,(xn,yn)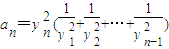 .证明当n≥2时,
.证明当n≥2时,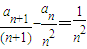 ;
;