题目内容
【题目】如图,抛物线![]() :
:![]() 与双曲线
与双曲线![]() :
:![]() (
(![]() ,
,![]() )有公共焦点
)有公共焦点![]() ,点
,点![]() 是曲线
是曲线![]() ,
,![]() 在在第一象限的交点,且
在在第一象限的交点,且![]() .
.
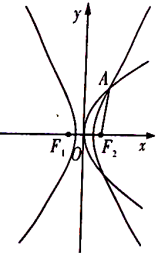
(1)求双曲线![]() 的方程;
的方程;
(2)以![]() 为圆心的圆
为圆心的圆![]() 与双曲线的一条渐进线相切,圆
与双曲线的一条渐进线相切,圆![]() .已知点
.已知点![]() ,过点
,过点![]() 作互相垂直分别与圆
作互相垂直分别与圆![]() 、圆
、圆![]() 相交的直线
相交的直线![]() 和
和![]() ,设
,设![]() 被圆
被圆![]() 解得的弦长为
解得的弦长为![]() ,
,![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .试探索
.试探索![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)借助题设条件运用双曲线的定义求解;(2)借助题设运用直线与圆的位置关系探求.
试题解析:
(1)∵抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,
,
∴双曲线![]() 的焦点为
的焦点为![]() ,
,![]() ,
,
设![]() 在抛物线
在抛物线![]() :
:![]() 上,且
上,且![]() ,
,
由抛物线的定义得![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
![]() ,
,
又∵点![]() 在双曲线上,由双曲线定义得
在双曲线上,由双曲线定义得![]() ,所以
,所以![]() ,
,
∴双曲线的方程为:![]() .
.
(2)![]() 为定值.下面给出说明:
为定值.下面给出说明:
设圆![]() 的方程为
的方程为![]() ,双曲线的渐近线方程为
,双曲线的渐近线方程为![]() .
.
∵圆![]() 与渐近线
与渐近线![]() 相切,∴圆
相切,∴圆![]() 的半径为
的半径为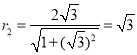 ,
,
故圆![]() :
:![]() .
.
依题意![]() 、
、![]() 的斜率存在且均不为零,
的斜率存在且均不为零,
所以设![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
设![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
∴点![]() 到直线
到直线![]() 的距离
的距离![]() ,点
,点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
∴直线![]() 被圆
被圆![]() 截得的弦长
截得的弦长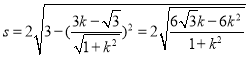 ,
,
直线![]() 被圆
被圆![]() 截得的弦长
截得的弦长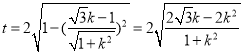 ,
,
∴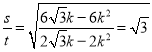 ,故
,故![]() 为定值
为定值![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
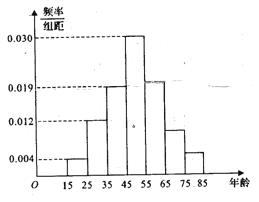
【题目】某校高三共有2000名学生参加广安市联考,现随机抽取100名学生的成绩(单位:分),并列成如下表所示的频数分布表:
组别 |
|
|
|
|
|
|
频数 | 6 | 18 | 28 | 26 | 17 | 5 |
(1)试估计该年级成绩![]() 分的学生人数;
分的学生人数;
(2)已知样本中成绩在![]() 中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.