题目内容
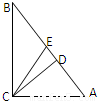
在三角形ABC中,E,F为AC的三等份点,D为BC中点,AD与BE,BF分别相交于点M,N,则AM:MN:ND的值为( )
| A、5:3:3 | B、4:3:2 | C、5:3:2 | D、5:3:4 |
分析:先过D点作DG∥AC,然后根据中位线定理可知DG=AE=
EC,进而可得到AM=DM,
然后连接DF则可得到ME为△ADF的中位线,同样可得到EM=
DF,再由DF为△CEB的中位线,从而可得到DF=
BE,进而可得到DF:BM=DN:MN=2:3,从而可知AM:MN:ND=5:3:2.
| 1 |
| 2 |
然后连接DF则可得到ME为△ADF的中位线,同样可得到EM=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:过D点作DG∥AC交BE于G则DG为△BCE的中位线
∴DG=AE=
EC
∴AM=DM
连接DF则ME为△ADF的中位线
∴EM=
DF
又∵DF为△CEB的中位线
∴DF=
BE
∴DF:BM=DN:MN=2:3
∴AM:MN:ND=5:3:2
故答案为C.
∴DG=AE=
| 1 |
| 2 |
∴AM=DM
连接DF则ME为△ADF的中位线
∴EM=
| 1 |
| 2 |
又∵DF为△CEB的中位线
∴DF=
| 1 |
| 2 |
∴DF:BM=DN:MN=2:3
∴AM:MN:ND=5:3:2
故答案为C.
点评:本题主要考查三角形中位线定理的应用,三角形的中位线定理在三角形中应用比较广泛,一定要熟练掌握.

练习册系列答案
相关题目
 如图在三角形ABC中,E为斜边AB的中点,CD⊥AB,AB=1,则
如图在三角形ABC中,E为斜边AB的中点,CD⊥AB,AB=1,则 ,
,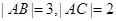 ,A=600,则
,A=600,则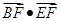 等于( )
等于( )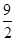 B.
B.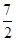 C.
C.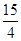 D.
D.
 的最大值是 .
的最大值是 .