Question

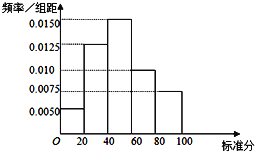
【题目】某学校社团为调查学生课余学习围棋的情况，随机抽取了100名学生进行调查．根据调查结果绘制的学生日均学习围棋时间的频率分布直方图如图所示，将日均学习围棋时间不低于40分钟的学生称为“围棋迷”．

根据已知条件完成下面的列联表，并据此资料判断能不能在犯错误的概率不超过0.05的前提下认为“围棋迷”与性别有关？

	非围棋迷	围棋迷	总计
男
女		10	55
总计

附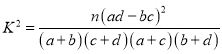：，其中．

	0.10	0.05	0.025	0.010	0.005	0.001
	2.706	3.841	5.024	6.635	7.879	10.828

Answer 1

【答案】列联表详见解析，不能在犯错误的概率不超过的前提下认为“围棋迷”与性别有关．

【解析】

列出二联表，计算观测值，与3.841比较大小得出结论；

解：由频率分布直方图可知，在抽取的人中，“围棋迷”有人，

从而残联表如下所示：

	非围棋迷	围棋迷	总计
男	30	15	45
女	45	10	55
总计	75	25	100

将残联表中的数据代入公式计算，得的观测值

，

因为，所以不能在犯错误的概率不超过的前提下认为“围棋迷”与性别有关．