Question

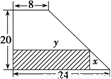
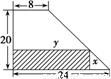
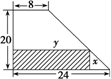某厂有许多形状为直角梯形的铁皮边角料，如图．为降低消耗，开源节流，现要从这些边角料上截取矩形铁片（如图中阴影部分）备用，当截取的矩形面积最大时，矩形两边长x、y应为（　　）

A．x=15，y=12

B．x=12，y=15

C．x=14，y=10

D．x=10，y=14

Answer 1

分析：由直角三角形相似得

24-y

24-8

=

x

20

，得x=

5

4

•（24-y），化简矩形面积S=xy的解析式为=-

5

4

（y-12）²+180，再利用二次函数的性质求出S 的最大值，以及取得最大值时x、y的值．

解答：解：由直角三角形相似得

24-y

24-8

=

x

20

，得x=

5

4

•（24-y），
∴矩形面积S=xy=-

5

4

（y-12）²+180，
∴当y=12时，S有最大值，此时x=15．
故选 A．

点评：本题主要考查三角形中的几何计算、二次函数的性质的应用，属于中档题．