题目内容
在三棱锥A—BCD中,AC=AB=DC=DB=2,AD=BC=1,求该三棱锥的体积.
思路分析:三棱锥的六条棱长都已知,且比较特殊,我们不难求得△ACB的面积,但点D在面ABC内的射影位置不明显,三棱锥的高比较难求.于是,我们以点A为原点,面ABC所在平面为xOy面,将AB置于Ox轴正半轴上,建立空间直角坐标系,问题便转化为求点D的坐标,而这不难用两点间的距离公式求解.
解:以点A为原点,面ABC所在平面为xOy面,将AB置于Ox轴的正半轴上,建立空间直角坐标系,如图4-3-2.
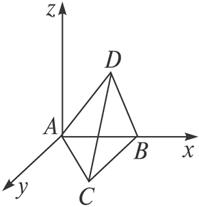
图4-3-2
AC=AB=2,BC=1,易求得S△ABC=![]() ×1×
×1×![]() .
.
A(0,0,0),B(2,0,0),C(![]() ,0).
,0).
设D(x,y,z).
由DA=1得x2+y2+z2=1.①
由DC=2,得(x-![]() )2+(y-
)2+(y-![]() )2+z2=4.②
)2+z2=4.②
由DB=2,得(x-2)2+y2+z2=4.③
由①③,得-4x+4=3,x=![]() .④
.④
将①④代入②,得1-![]() y=4,y=
y=4,y=![]() .⑤
.⑤
将④⑤代入①,得![]() +z2=1,
+z2=1,
∴z2=![]() ,z=
,z=![]() .
.
∴D点到平面ACB的距离为![]() ,三棱锥的体积为
,三棱锥的体积为![]() .
.
绿色通道:本题采用建立空间直角坐标系,将问题转化为求D点的坐标问题的方法,避开了逻辑推理与空间想象而进行代数运算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且长度均为1,E为BC中点,则下列结论正确的是( )
如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且长度均为1,E为BC中点,则下列结论正确的是( ) 在三棱锥A-BCD中,AB=4,CD=2,且异面直线AB、CD所成的角为60°,若M、N分别是AD、BC的中点,则MN=
在三棱锥A-BCD中,AB=4,CD=2,且异面直线AB、CD所成的角为60°,若M、N分别是AD、BC的中点,则MN= (2011•渭南三模)在三棱锥A-BCD中,BD=BC=1,BD⊥BC,DE⊥AB,AD=2,AD⊥平面BCD.
(2011•渭南三模)在三棱锥A-BCD中,BD=BC=1,BD⊥BC,DE⊥AB,AD=2,AD⊥平面BCD. 如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜
如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜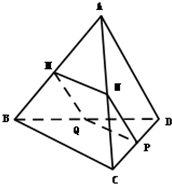 如图,在三棱锥A-BCD中,平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点,且MN=PQ.
如图,在三棱锥A-BCD中,平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点,且MN=PQ.