题目内容
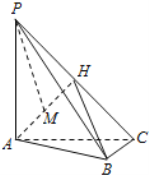
【题目】如图,在以![]() 为顶点,母线长为
为顶点,母线长为![]() 的圆锥中,底面圆
的圆锥中,底面圆![]() 的直径
的直径![]() 长为2,
长为2,![]() 是圆
是圆![]() 所在平面内一点,且
所在平面内一点,且![]() 是圆
是圆![]() 的切线,连接
的切线,连接![]() 交圆
交圆![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
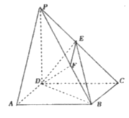
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,当二面角
,当二面角![]() 的大小为
的大小为![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)由![]() 是圆
是圆![]() 的直径,
的直径,![]() 与圆
与圆![]() 切于点
切于点![]() ,可得
,可得![]() ,
,
由![]() 底面圆
底面圆![]() ,可得
,可得![]() ,利用线面垂直的判定定理可知,
,利用线面垂直的判定定理可知,![]() 平面
平面![]() ,即可推出
,即可推出![]() .又在
.又在![]() 中,
中,![]() ,可推出
,可推出![]() ,利用线面垂直的判定定理可证
,利用线面垂直的判定定理可证![]() 平面
平面![]() ,从而利用面面垂直的判定定理可证出平面
,从而利用面面垂直的判定定理可证出平面![]() 平面
平面![]() .
.
(2)由![]() ,
,![]() ,可知
,可知![]() 为二面角
为二面角![]() 的平面角,
的平面角,
即![]() ,建立空间直角坐标系,易知
,建立空间直角坐标系,易知![]() ,
,
求得点的坐标如下;![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,
由(1)知![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设平面![]() 的法向量为
的法向量为![]() ,
,
![]() ,
,![]() ,
,
通过![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
可求出平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴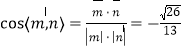 .
.
∴ 平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.
解:(1)![]() 是圆
是圆![]() 的直径,
的直径,![]() 与圆
与圆![]() 切于点
切于点![]() ,
,![]()
![]() 底面圆
底面圆![]() ,∴
,∴![]()
![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() .
.
又∵在![]() 中,
中,![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() 平面
平面![]() ,从而平面
,从而平面![]() 平面
平面![]() .
.
(2)∵ ![]() ,
,![]() ,∴
,∴![]() 为二面角
为二面角![]() 的平面角,
的平面角,
∴ ![]() ,
,
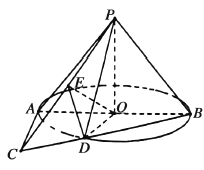
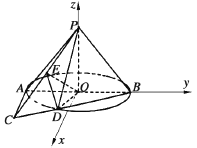
如图建立空间直角坐标系,易知![]() ,
,
则![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,
由(1)知![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设平面![]() 的法向量为
的法向量为![]() ,
,
![]() ,
,![]() ,
,
∵ ![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
∴ 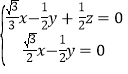 ,即
,即![]()
故平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴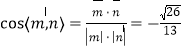 .
.
∴ 平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.

【题目】为了研究高中学生对乡村音乐的态度(喜欢和不喜欢两种态度)与性别的关系,运用2×2列联表进行独立性检验,经计算K2=8.01,附表如下:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参照附表,得到的正确的结论是( )
A. 有99%以上的把握认为“喜欢乡村音乐与性别有关”
B. 有99%以上的把握认为“喜欢乡村音乐与性别无关”
C. 在犯错误的概率不超过0.1%的前提下,认为“喜欢乡村音乐与性别有关”
D. 在犯错误的概率不超过0.1%的前提下,认为“喜欢乡村音乐与性别无关”