题目内容
17．
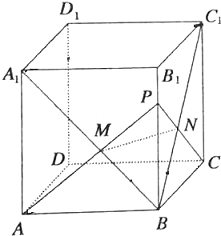如图，在长方体ABCD-A1B1C1D1中，点P∈BB1（P不与B，B1重合）．PA∩A1B=M，PC∩BC1=N．求证：MN∥平面ABCD．
分析 由已知得AC∥A1C1，从而得到AC∥平面A1BC1，再由平面A1BC1∩平面PAC=MN，得到AC∥MN，由此能证明MN∥平面ABCD．
解答 证明：如图，连接AC、A1C1，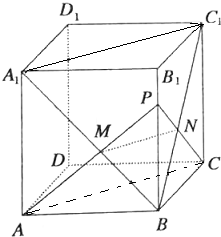
在长方体ABCD-A1B1C1D1中，AA1∥CC1，且AA1=CC1，
∴四边形ACC1A1是平行四边形．∴AC∥A1C1．
∵AC?平面A1BC1，A1C1?平面A1BC1，
∴AC∥平面A1BC1．
∵AC?平面PAC，平面A1BC1∩平面PAC=MN，∴AC∥MN．
∵MN?平面ABCD，AC?平面ABCD，
∴MN∥平面ABCD．
点评 本题考查直线与平面平行的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
7．某几何体的三视图如图所示，则该几何体的体积为（ ）
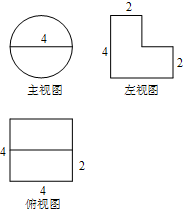
| A． | 4π | B． | 8π | C． | 12π | D． | 16π |
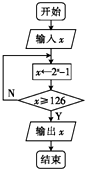
5．执行如图所示的程序框图，则输出的结果为（ ）
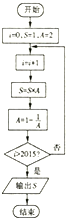
| A． | 2 | B． | 1 | C． | -1 | D． | -2 |
2．已知α，β是两个不同的平面，有下列三个条件：
①存在一个平面γ，γ⊥α，γ∥β；
②存在一条直线a，a?α，a⊥β；
③存在两条垂直的直线a，b，a⊥β，b⊥α．
其中，所有能称为“α⊥β”的充要条件的序号是（ ）
①存在一个平面γ，γ⊥α，γ∥β；
②存在一条直线a，a?α，a⊥β；
③存在两条垂直的直线a，b，a⊥β，b⊥α．
其中，所有能称为“α⊥β”的充要条件的序号是（ ）
| A． | ① | B． | ② | C． | ③ | D． | ①③ |
7．
如图所示的算法流程图中，若f（x）=lnx，g（x）=log2x，则h（4）的值等于（ ）
如图所示的算法流程图中，若f（x）=lnx，g（x）=log2x，则h（4）的值等于（ ）| A． | 1 | B． | -1 | C． | 2 | D． | ln4 |