题目内容
某工厂生产甲、乙两种产品,生产每一吨产品所需的劳动力、煤、电耗及利润如下表:产品品种 | 劳动力(个) | 煤(t) | 电(千瓦) | 利润(万元/t) |
甲产品 | 4 | 9 | 3 | 7 |
乙产品 | 5 | 4 | 10 | 12 |
因条件限制,该工厂仅有200个劳动力,煤360 t,供电局只供电300千瓦,试问该工厂生产甲、乙两种产品多少吨才能获得最大利润?
思路解析:根据题目所列表格,列出所有限制条件,确定目标函数,然后按线性规划的方法求解. 解:设工厂生产甲、乙两种产品分别为x吨、y吨,总利润为z万元,则 作出不等式组所表示的平面区域如图,作一组平行直线l:7x+12y=z. 当直线经过4x+5y=200与直线3x+10y=300的交点P(20,24)时,z达到最大值?. 故该厂生产甲种产品20 t,乙种产品24 t时能使利润达到最大.
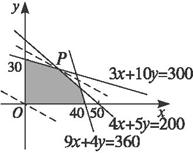
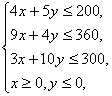 目标函数为z=7x+12y.
目标函数为z=7x+12y.
 练习册系列答案
练习册系列答案
1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案

完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案
相关题目
 18、某工厂生产甲、乙两种产品,每种产品都是经过第一道和第二道工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级,对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品
18、某工厂生产甲、乙两种产品,每种产品都是经过第一道和第二道工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级,对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品