题目内容
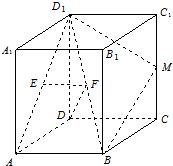 如图,已知长方体ABCD-A1B1C1D1的底面ABCD为正方形,E为线段AD1的中点,F为线段BD1的中点.
如图,已知长方体ABCD-A1B1C1D1的底面ABCD为正方形,E为线段AD1的中点,F为线段BD1的中点.(1)求证:EF∥平面ABCD;
(2)设M为线段C1C的中点,当
| D1D | AD |
并说明理由.
分析:(1)要证:EF∥平面ABCD,只需证明EF∥AB,由直线与平面平行的判定定理可知EF∥平面ABCD.
(2)F为线段BD1的中点,当
=
时,易证DF⊥BD1,再证MF⊥平面BB1D1D,就能证明FM⊥DF,即可证明DF⊥平面D1MB.
(2)F为线段BD1的中点,当
| D1D |
| AD |
| 2 |
解答:解:(1)∵E为线段AD1的中点,F为线段BD1的中点,
∴EF∥AB,
∵EF?平面ABCD,AB?平面ABCD,
∴EF∥面ABCD.
(2)当
=
时,DF⊥平面D1MB.
证明如下:连接AC,BD.
设AC与BD交于点O、连接OF,FM.在长方体中,
∵O是BD的中点,
∴OF∥DD1且OF=
DD1、而CM∥DD1且CM=
DD1.
∴OF∥CM且OF=CM,
∴四边形OCMF是平行四边形.
∴FM∥OC.
∵DD1⊥平面ABCD,
∴D1D⊥OC,而OC⊥BD,
∴OC⊥平面BB1D1D,
∴OC⊥DF,
∴FM⊥DF.
∵D1D=
AD,
∴D1D=BD.
∵F为BD1的中点,
∴DF⊥BD1.
∵FM∩BD1=F,
∴DF⊥平面BD1M.
∴EF∥AB,
∵EF?平面ABCD,AB?平面ABCD,
∴EF∥面ABCD.
(2)当
| D1D |
| AD |
| 2 |
证明如下:连接AC,BD.
设AC与BD交于点O、连接OF,FM.在长方体中,
∵O是BD的中点,
∴OF∥DD1且OF=
| 1 |
| 2 |
| 1 |
| 2 |
∴OF∥CM且OF=CM,
∴四边形OCMF是平行四边形.
∴FM∥OC.
∵DD1⊥平面ABCD,
∴D1D⊥OC,而OC⊥BD,
∴OC⊥平面BB1D1D,
∴OC⊥DF,
∴FM⊥DF.
∵D1D=
| 2 |
∴D1D=BD.
∵F为BD1的中点,
∴DF⊥BD1.
∵FM∩BD1=F,
∴DF⊥平面BD1M.
点评:本题考查直线与平面平行和垂直的判断,考查学生逻辑思维能力,空间想象能力,是难题.

练习册系列答案
相关题目
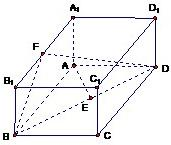 如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点.
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点. 如图,已知长方体ABCD-A1B1C1D1中,AB=
如图,已知长方体ABCD-A1B1C1D1中,AB= 如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE.
如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE. 如图,已知长方体ABCD-A′B′C′D′中,AB=2
如图,已知长方体ABCD-A′B′C′D′中,AB=2 (2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F
(2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F