题目内容
已知函数f(x)=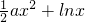 .
.
(1)当a=- 时,求函数f(x)在[1,e]上的最大值、最小值;
时,求函数f(x)在[1,e]上的最大值、最小值;
(2)求f(x)的单调区间.
解:(1)∵f(x)=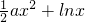 .
.
当a=- 时,f(x)=-
时,f(x)=-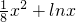
∴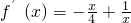 =
=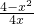 =
=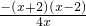
令f′(x)=0可得x1=2,x2=-2
当x∈[1,2],f′(x)>0,当x∈[2,e]时,f′(x)<0
∴函数在区间[1,e]上,有x1=2时,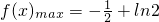 ,f(x)min=min{f(1),f(e)}
,f(x)min=min{f(1),f(e)}
而f(1)=-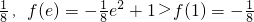
∴f(x)min=-
(2)∵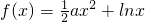
∴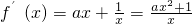
①当a≥0时,由f′(x)>0可得,x>0,由f′(x)<0可得x<0
又x>0
∴f(x)在(0,+∞)单调递增
②当a<0时,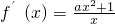 =
=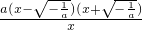
由f′(x)>0可得,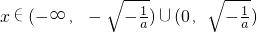
由f′(x)<0可得,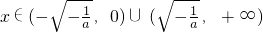 ,又x>0
,又x>0
∴f(x)的单调递增区间(0, ),减区间(
),减区间(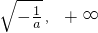 )
)
分析:(1)由f(x)=-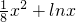 ,对函数求导可得
,对函数求导可得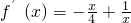 =
=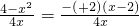 ,从而可求函数在区间[1,e]上单调性进而可求函数的最大值域最小值
,从而可求函数在区间[1,e]上单调性进而可求函数的最大值域最小值
(2)对函数求导,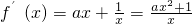
①当a≥0时,分别由f′(x)>0,f′(x)<0可求函数的单调区间
②当a<0时,由f′(x)>0,f′(x)<0可求函数单调区间
点评:本题主要考查了函数的导数 求解函数的极值及函数的最值,利用导数判断函数的单调区间,解题中要注意分类讨论思想的应用.
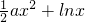 .
.当a=-
 时,f(x)=-
时,f(x)=-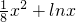
∴
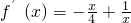 =
=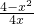 =
=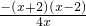
令f′(x)=0可得x1=2,x2=-2
当x∈[1,2],f′(x)>0,当x∈[2,e]时,f′(x)<0
∴函数在区间[1,e]上,有x1=2时,
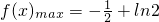 ,f(x)min=min{f(1),f(e)}
,f(x)min=min{f(1),f(e)}而f(1)=-
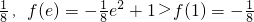
∴f(x)min=-

(2)∵
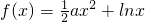
∴
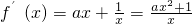
①当a≥0时,由f′(x)>0可得,x>0,由f′(x)<0可得x<0
又x>0
∴f(x)在(0,+∞)单调递增
②当a<0时,
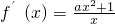 =
=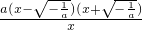
由f′(x)>0可得,
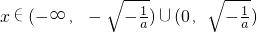
由f′(x)<0可得,
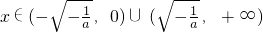 ,又x>0
,又x>0∴f(x)的单调递增区间(0,
 ),减区间(
),减区间(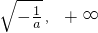 )
)分析:(1)由f(x)=-
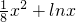 ,对函数求导可得
,对函数求导可得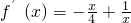 =
=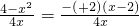 ,从而可求函数在区间[1,e]上单调性进而可求函数的最大值域最小值
,从而可求函数在区间[1,e]上单调性进而可求函数的最大值域最小值(2)对函数求导,
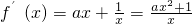
①当a≥0时,分别由f′(x)>0,f′(x)<0可求函数的单调区间
②当a<0时,由f′(x)>0,f′(x)<0可求函数单调区间
点评:本题主要考查了函数的导数 求解函数的极值及函数的最值,利用导数判断函数的单调区间,解题中要注意分类讨论思想的应用.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|