题目内容
设
，函数
.
（1）当
时，求函数
的单调增区间；
（2）若
时，不等式
恒成立，实数
的取值范围.
【答案】
（1）当
时，单调增区间为
.（2）
.
【解析】(1)先去绝对值转化为分段函数，
，然后利用导数分段研究单调区间.
（2）先去约对值，分两类进行研究当
时，
;当
时，
，然后利用导数分别转化为不等式恒成立问题进行研究，最后求得的参数a的范围求交集即可.
（1）当时，
…………（2分）
当
时，
，
在
内单调递增；
当时，
恒成立，故在
内单调递增；
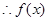的单调增区间为.
…………（5分）
（2）①当时，，
，
恒成立，在
上增函数.
故当
时，
.
…………（6分）
②当时，，
（Ⅰ）当
，即
时，
在
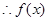时为正数，所以在区间
上为增函数.故当
时，
，且此时
…………（7分）
（Ⅱ）当
，即
时，在
时为负数，在
时为正数，所以在区间
上为减函数，在
上为增函数.故当
时，
，且此时
.
…………（8分）
（Ⅲ）当
，即
时，在时为负数，所以在区间
上为减函数，故当时，.
所以函数
的最小值为
.…………（9分）
由条件得
此时；或
，此时
；或
，此时无解.
综上，.
…………（12分）
练习册系列答案
相关题目
．
。
的极值；
2时，讨论函数
成立，求
．
的极小值；
，x∈[-1，1]，求
的最大值F（a）．