题目内容
在平面直角坐标系xOy中,“直线y=x+b,b∈R与曲线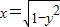 相切”的充要条件是 .
相切”的充要条件是 .
【答案】分析:将曲线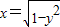 化简,得它是单位圆位于y轴右侧的部分,直线y=x+b与曲线
化简,得它是单位圆位于y轴右侧的部分,直线y=x+b与曲线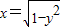 相切,即原点到直线的距离等于1,再结合切点的位置即可得到b的值,从而得到所求的充要条件.
相切,即原点到直线的距离等于1,再结合切点的位置即可得到b的值,从而得到所求的充要条件.
解答:解:曲线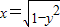 化简,得x2+y2=1(x≥0)
化简,得x2+y2=1(x≥0)
∴曲线表示单位圆位于y轴右侧的部分
∵直线y=x+b与曲线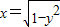 相切
相切
∴圆心(0,0)到直线x-y+b=0的距离等于1,
即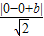 =1,解得b=
=1,解得b=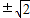 ,
,
∵切点位于第四象限,
∴b<0,可得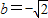 (舍正)
(舍正)
因此,“直线y=x+b,b∈R与曲线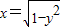 相切”的充要条件是
相切”的充要条件是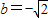
故答案为: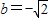
点评:本题给出直线与单位圆相切,求参数的值,着重考查了曲线与方程、直线与圆的位置关系和充要条件等知识,属于基础题.
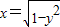 化简,得它是单位圆位于y轴右侧的部分,直线y=x+b与曲线
化简,得它是单位圆位于y轴右侧的部分,直线y=x+b与曲线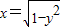 相切,即原点到直线的距离等于1,再结合切点的位置即可得到b的值,从而得到所求的充要条件.
相切,即原点到直线的距离等于1,再结合切点的位置即可得到b的值,从而得到所求的充要条件.解答:解:曲线
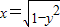 化简,得x2+y2=1(x≥0)
化简,得x2+y2=1(x≥0)∴曲线表示单位圆位于y轴右侧的部分
∵直线y=x+b与曲线
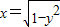 相切
相切∴圆心(0,0)到直线x-y+b=0的距离等于1,
即
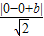 =1,解得b=
=1,解得b=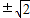 ,
,∵切点位于第四象限,
∴b<0,可得
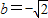 (舍正)
(舍正)因此,“直线y=x+b,b∈R与曲线
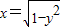 相切”的充要条件是
相切”的充要条件是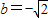
故答案为:
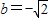
点评:本题给出直线与单位圆相切,求参数的值,着重考查了曲线与方程、直线与圆的位置关系和充要条件等知识,属于基础题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是