题目内容
“α=
”是“cos2α=
”的( )
| π |
| 6 |
| 1 |
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
分析:当α=
时,cos2α=cos
=
;反之,当cos2α=
时,α=kπ+
,k∈Z,或α=kπ-
,k∈Z.所以“α=
”是“cos2α=
”的充分而不必要条件.
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
解答:解:当α=
时,cos2α=cos
=
,
反之,当cos2α=
时,可得2α=2kπ+
?α=kπ+
,k∈Z,或2α=2kπ-
?α=kπ-
,k∈Z,
“α=
”是“cos2α=
”的充分而不必要条件
故应选A.
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
反之,当cos2α=
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
“α=
| π |
| 6 |
| 1 |
| 2 |
故应选A.
点评:本题考查充分条件、必要条件、充分条件,解题时要认真审题,仔细解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤. 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E: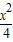
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.
 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E:
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.