题目内容
(2009北京西城高三抽样测试,理18)已知数列{an}的前n项和为Sn,a1=1,数列{an+Sn}是公差为2的等差数列.
(1)求a2,a3;
(2)证明数列{an-2}为等比数列;
(3)求数列{nan}的前n项和Tn.
(1)解:∵数列{an+Sn}是公差为2的等差数列,
∴(an+1+Sn+1)-(an+Sn)=2,
即![]() .
.
∵a1=1,∴![]() .
.
(2)证明:由题意,得a1-2=-1,
∵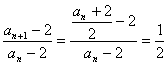 ,
,
∴{an-2}是首项为-1,公比为![]() 的等比数列.
的等比数列.
(3)解:由(2)得an-2=-(![]() )n-1,
)n-1,
∴nan=2n-n·(![]() )n-1.
)n-1.
∴Tn=(2-1)+(4-2·![]() )+[6-3·(
)+[6-3·(![]() )2]+…+[2n-n·(
)2]+…+[2n-n·(![]() )n-1].
)n-1].
∴Tn=(2+4+6+…+2n)-[1+2·![]() +3·(
+3·(![]() )2+…+n·(
)2+…+n·(![]() )n-1].
)n-1].
设![]() ,①
,①
∴![]() .②
.②
由①-②,得![]() ,
,
∴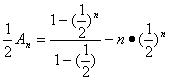 .
.
∴An=4-(n+2)·(![]() )n-1.
)n-1.
∴![]() .
.

练习册系列答案
相关题目
 (2009北京卷理)若正四棱柱
(2009北京卷理)若正四棱柱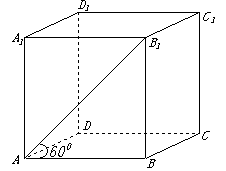 (2009北京卷理)若正四棱柱
(2009北京卷理)若正四棱柱