题目内容
7.已知圆C的极坐标方程为ρ2+2$\sqrt{2}$ρsin(θ-$\frac{π}{4}$)-4=0,求圆C的半径.分析 先根据x=ρcosθ,y=ρsinθ,求出圆的直角坐标方程,求出半径.
解答 解:圆的极坐标方程为ρ2+2$\sqrt{2}$ρsin(θ-$\frac{π}{4}$)-4=0,可得ρ2-2ρcosθ+2ρsinθ-4=0,
化为直角坐标方程为x2+y2-2x+2y-4=0,
化为标准方程为(x-1)2+(y+1)2=6,
圆的半径r=$\sqrt{6}$.
点评 本题主要考查把极坐标方程化为直角坐标方程的方法,以及求点的极坐标的方法,关键是利用公式x=ρcosθ,y=ρsinθ,比较基础,

练习册系列答案
相关题目
19.根据如图给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是( )


| A. | 逐年比较,2008年减少二氧化硫排放量的效果最显著 | |
| B. | 2007年我国治理二氧化硫排放显现成效 | |
| C. | 2006年以来我国二氧化硫年排放量呈减少趋势 | |
| D. | 2006年以来我国二氧化硫年排放量与年份正相关 |
16.设函数f(x)=ex(2x-1)-ax+a,其中a<1,若存在唯一的整数x0使得f(x0)<0,则a的取值范围是( )
| A. | [$-\frac{3}{2e},1$) | B. | [$-\frac{3}{2e},\frac{3}{4}$) | C. | [$\frac{3}{2e},\frac{3}{4}$) | D. | [$\frac{3}{2e},1$) |
17.函数f(x)=log2(x2+2x-3)的定义域是( )
| A. | [-3,1] | B. | (-3,1) | C. | (-∞,-3]∪[1,+∞) | D. | (-∞,-3)∪(1,+∞) |
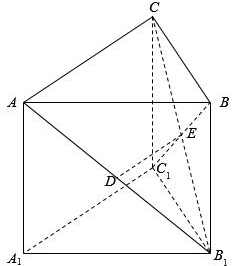 如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.
如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.