题目内容
已知|a|=6,|b|=8,且|a+b|=|a-b|,求|a-b|.
思路分析:从题目条件中挖掘平行四边形所满足的几何特征.
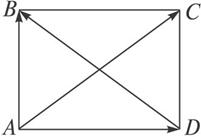
解:如图,设|![]() |=a,|
|=a,|![]() |=b,
|=b,
以AB,AD为邻边作![]() ABCD,
ABCD,
则![]() =a+b,
=a+b,![]() =a-b.
=a-b.
∵|a+b|=|a-b|,
即|![]() |=|
|=|![]() |,
|,
∴![]() ABCD为矩形,故AD⊥AB.
ABCD为矩形,故AD⊥AB.
在Rt△DAB中,|![]() |=6,|
|=6,|![]() |=8,
|=8,
由勾股定理,得
|![]() =10.
=10.
∴|a+b|=|a-b|=10.

练习册系列答案
相关题目
题目内容
已知|a|=6,|b|=8,且|a+b|=|a-b|,求|a-b|.
思路分析:从题目条件中挖掘平行四边形所满足的几何特征.

解:如图,设|![]() |=a,|
|=a,|![]() |=b,
|=b,
以AB,AD为邻边作![]() ABCD,
ABCD,
则![]() =a+b,
=a+b,![]() =a-b.
=a-b.
∵|a+b|=|a-b|,
即|![]() |=|
|=|![]() |,
|,
∴![]() ABCD为矩形,故AD⊥AB.
ABCD为矩形,故AD⊥AB.
在Rt△DAB中,|![]() |=6,|
|=6,|![]() |=8,
|=8,
由勾股定理,得
|![]() =10.
=10.
∴|a+b|=|a-b|=10.
