题目内容
已知α为第二象限的角, ,求下列各式的值:
,求下列各式的值:
(1)sinα;
(2) ;
;
(3) .
.
解:(1)将已知式平方,得
cos2 +2sin
+2sin cos
cos +sin2
+sin2 =
= ,即
,即 ,因此
,因此 .…(4分)
.…(4分)
(2)∵α为第二象限角,得
 ,
,
所以 =
= .…(8分)
.…(8分)
(3)∵( )2+(
)2+( )2=2,
)2=2,
∴( )2=2-
)2=2- =
=
又∵α为第二象限角,cosα= =(
=( )(
)( )<0
)<0
∴ .(舍负)…(12分)
.(舍负)…(12分)
分析:(1)将已经式平方展开,再结合同角三角函数的平方关系和二倍角的正弦公式,即可得到sinα的值;
(2)用同角三角函数基本关系求出cosα的值,再用两角和的正弦公式,即可求出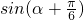 的值;
的值;
(3)根据同角三角函数关系的平方关系,可以算出( )2的值,再由α为第二象限的角,即可得到
)2的值,再由α为第二象限的角,即可得到 为正数,得到所求的值.
为正数,得到所求的值.
点评:本题考查了同角三角函数的基本关系、二倍角的正弦公式、两角和的正弦公式等三角函数化简求值的知识,属于基础题.
cos2
 +2sin
+2sin cos
cos +sin2
+sin2 =
= ,即
,即 ,因此
,因此 .…(4分)
.…(4分)(2)∵α为第二象限角,得
 ,
,所以
 =
= .…(8分)
.…(8分)(3)∵(
 )2+(
)2+( )2=2,
)2=2,
∴(
 )2=2-
)2=2- =
=
又∵α为第二象限角,cosα=
 =(
=( )(
)( )<0
)<0∴
 .(舍负)…(12分)
.(舍负)…(12分)分析:(1)将已经式平方展开,再结合同角三角函数的平方关系和二倍角的正弦公式,即可得到sinα的值;
(2)用同角三角函数基本关系求出cosα的值,再用两角和的正弦公式,即可求出
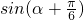 的值;
的值;(3)根据同角三角函数关系的平方关系,可以算出(
 )2的值,再由α为第二象限的角,即可得到
)2的值,再由α为第二象限的角,即可得到 为正数,得到所求的值.
为正数,得到所求的值.点评:本题考查了同角三角函数的基本关系、二倍角的正弦公式、两角和的正弦公式等三角函数化简求值的知识,属于基础题.

练习册系列答案
相关题目
 ,求tan2α
,求tan2α 且α为第二象限的角,则tanα= .
且α为第二象限的角,则tanα= . ,求tan2α
,求tan2α