Question

【题目】已知椭圆E：=1（a＞b＞0）的焦距为2 ， 且该椭圆经过点(,)．
（Ⅰ）求椭圆E的方程；
（Ⅱ）经过点P（﹣2，0）分别作斜率为k1 ， k2的两条直线，两直线分别与椭圆E交于M，N两点，当直线MN与y轴垂直时，求k1k2的值．

Answer 1

【答案】解：（Ⅰ）由题意得，2c=2，=1；
解得，a2=4，b2=1；
故椭圆E的方程为+y2=1；
（Ⅱ）由题意知，当k1=0时，M点的纵坐标为0，
直线MN与y轴垂直，
则点N的纵坐标为0，
故k2=k1=0，这与k2≠k1矛盾．
当k1≠0时，直线PM：y=k1（x+2）；
由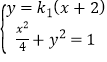得，
（+4）y2﹣=0；
解得，yM=；
∴M（，），
同理N（，），
由直线MN与y轴垂直，则=；
∴（k2﹣k1）（4k2k1﹣1）=0，
∴k2k1=．
【解析】（Ⅰ）由题意得，2c=2 ， =1；从而求椭圆E的方程；
（Ⅱ）由题意知，当k1=0时，M点的纵坐标为0，点N的纵坐标为0，故不成立；当k1≠0时，直线PM：y=k1（x+2）；联立方程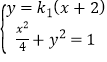得（+4）y2﹣=0；从而解得yM=；可得M（ ， ），N（ ， ）；从而可得（k2﹣k1）（4k2k1﹣1）=0，从而解得．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：，焦点在y轴：．