题目内容
如图是函数y=f（x）的图象，f（f（2））的值为
- A.3
- B.4
- C.5
- D.6
C
分析：当0≤x≤3时，根据 y=f（x）=2x求得f（2）=4．当3＜x≤9时，根据f（x）=9-x，求得 f（ f（2））=f（4）的值．
解答：由图象可得，当0≤x≤3时，y=f（x）=2x，∴f（2）=4．
当3＜x≤9时，由 y-0=
（x-9），可得 y=f（x）=9-x，故 f（ f（2））=f（4）=9-4=5，
故选C．
点评：本题主要考查利用分段函数求函数的值，体现了分类讨论的数学思想，属于基础题．
分析：当0≤x≤3时，根据 y=f（x）=2x求得f（2）=4．当3＜x≤9时，根据f（x）=9-x，求得 f（ f（2））=f（4）的值．
解答：由图象可得，当0≤x≤3时，y=f（x）=2x，∴f（2）=4．
当3＜x≤9时，由 y-0=
（x-9），可得 y=f（x）=9-x，故 f（ f（2））=f（4）=9-4=5，故选C．
点评：本题主要考查利用分段函数求函数的值，体现了分类讨论的数学思想，属于基础题．
练习册系列答案
相关题目
4、如图是函数y=f（x）的图象，则下列说法正确的是（ ）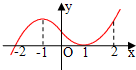
如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：
如图是函数y=f（x）的导函数y=f′（x）的图象，下列说法错误的是（ ）
（2012•茂名一模）如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：
如图是函数y=f（x）的导函数y=f′（x）的图象，下列说法正确的是