题目内容
已知数列 的前
的前 项和
项和 ,正项等比数列
,正项等比数列 中,
中, ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
D
解析试题分析:法一:因为 ,所以
,所以 ,
, ,验证可知
,验证可知 均不符合,故答案为
均不符合,故答案为 .
.
法二:因为 ,所以
,所以 ,又
,又 ,即
,即 ,∴
,∴ ,
, .所以数列
.所以数列 的通项公式是
的通项公式是 ,所以
,所以 .故选
.故选 .
.
考点:1.等比数列的通项公式;2.对数的计算.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
已知各项均为正数的等比数列{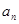 }中,
}中,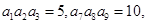 则
则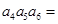 ( )
( )
A.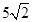 | B.7 | C.6 | D.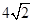 |
已知各项均为正数的等比数列 ,
,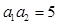 ,
, ,则
,则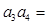 ( )
( )
A.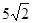 | B.7 | C.6 | D.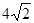 |
在等比数列 中,若
中,若 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知等比数列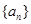 的公比
的公比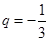 ,则
,则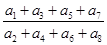 等于( )
等于( )
A. | B.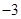 | C.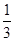 | D.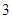 |
若公比为2且各项均为正数的等比数列 中,
中, ,则
,则 的值等于( )
的值等于( )
| A.2 | B.4 | C.8 | D.16 |
设等比数列 的前
的前 项和为
项和为 ,若
,若 ,
, ,则
,则 等于 ( )
等于 ( )
| A.16 | B.31 | C.32 | D.63 |
己知{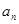 }是各项均为正数的等比数列,
}是各项均为正数的等比数列,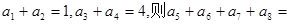
| A.80 | B.20 | C.32 | D.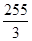 |
设首项为 ,公比为
,公比为 的等比数列
的等比数列 的前
的前 项和为
项和为 ,则( )
,则( )
A. | B. | C. | D. |