题目内容
曲线y=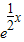 在点(4,e2)处的切线与坐标轴所围三角形的面积为( )
在点(4,e2)处的切线与坐标轴所围三角形的面积为( )A.
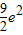
B.4e2
C.2e2
D.e2
【答案】分析:利用导数求曲线上点切线方程,求直线与x轴,与y轴的交点,然后求切线与坐标轴所围三角形的面积.
解答:解:∵曲线y=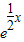 ,
,
∴y′=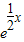 ×
× ,切线过点(4,e2)
,切线过点(4,e2)
∴f(x)|x=4= e2,
e2,
∴切线方程为:y-e2= e2(x-4),
e2(x-4),
令y=0,得x=2,与x轴的交点为:(2,0),
令x=0,y=-e2,与y轴的交点为:(0,-e2),
∴曲线y=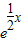 在点(4,e2)处的切线与坐标轴所围三角形的面积s=
在点(4,e2)处的切线与坐标轴所围三角形的面积s= ×2×|-e2|=e2,
×2×|-e2|=e2,
故选D.
点评:此题主要考查利用导数求曲线上点切线方程,解此题的关键是对曲线y=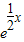 能够正确求导,此题是一道基础题.
能够正确求导,此题是一道基础题.
解答:解:∵曲线y=
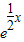 ,
,∴y′=
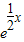 ×
× ,切线过点(4,e2)
,切线过点(4,e2)∴f(x)|x=4=
 e2,
e2,∴切线方程为:y-e2=
 e2(x-4),
e2(x-4),令y=0,得x=2,与x轴的交点为:(2,0),
令x=0,y=-e2,与y轴的交点为:(0,-e2),
∴曲线y=
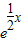 在点(4,e2)处的切线与坐标轴所围三角形的面积s=
在点(4,e2)处的切线与坐标轴所围三角形的面积s= ×2×|-e2|=e2,
×2×|-e2|=e2,故选D.
点评:此题主要考查利用导数求曲线上点切线方程,解此题的关键是对曲线y=
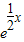 能够正确求导,此题是一道基础题.
能够正确求导,此题是一道基础题. 
练习册系列答案
相关题目