题目内容
(2013•南京二模)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知直线l:
(t为参数)和曲线C:
(t为参数).若P是曲线C上任意一点,求点P到直线l的距离的最小值及此时点P的坐标.
在平面直角坐标系xOy中,已知直线l:
|
|
分析:分别化直线l和曲线C的参数方程为普通方程,联立方程组后方程组无解可知直线和曲线相离,由导数求出和直线平行且与曲线相切的直线与曲线的切点,再由点到直线的距离公式求解.
解答:解:由直线l:
,得直线l的普通方程为2x+y-1=0,
由曲线C:
,得曲线C的普通方程为y=x2-2x+2.
∵方程组
无解,∴直线l和曲线C没有公共点.
由y=x2-2x+2,得y′=2x-2,再令2x-2=-2,得x=0,代入曲线y=x2-2x+2,得y=2.
∴当点P为(0,2)时,它到直线l的距离最小,最小距离为
=
.
|
由曲线C:
|
∵方程组
|
由y=x2-2x+2,得y′=2x-2,再令2x-2=-2,得x=0,代入曲线y=x2-2x+2,得y=2.
∴当点P为(0,2)时,它到直线l的距离最小,最小距离为
| |2-1| | ||
|
| ||
| 5 |
点评:本题考查了参数方程化普通方程,考查了点到直线的距离公式,考查了数学转化思想方法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
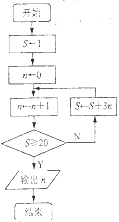 (2013•南京二模)如图是一个算法流程图,其输出的n的值是
(2013•南京二模)如图是一个算法流程图,其输出的n的值是