题目内容
3.将一本书打开后竖立在桌面α上(如图),P,Q分别为AC,BE上的点,且AP=BQ.求证:PQ∥平面α.
分析 连结CQ,交BF于M,连结AM,由平行线分线段成比例定理及其推论能得到PQ∥AM,由此能证明PQ∥平面α.
解答  解:连结CQ,交BF于M,连结AM,
解:连结CQ,交BF于M,连结AM,
∵AP=BQ,AC=BE,∴PC=QE,
∵BF∥CE,
∴$\frac{BQ}{QE}=\frac{MQ}{QC}=\frac{AP}{PC}$,
∴PQ∥AM,
∵AM?面α,PQ?面α,
∴PQ∥平面α.
点评 本题考查线面平行的证明,是基础题,解题时要认真审题,注意平行线分线段成比例定理及其推论和线面平行判定定理的合理运用.

练习册系列答案
相关题目
14.由五个面围成的多面体,其中上、下两个面是相似三角形,其余三个面都是梯形,并且这些梯形的腰延长后能相交于一点,则该多面体是( )
| A. | 三棱柱 | B. | 三棱台 | C. | 三棱锥 | D. | 四棱锥 |
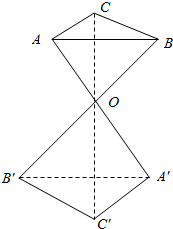 如图,△ABC和△A′B′C′的对应顶点的连线AA′,BB′,CC′交于同一点O,且$\frac{AO}{OA′}=\frac{BO}{OB′}=\frac{CO}{OC′}=\frac{2}{3}$.
如图,△ABC和△A′B′C′的对应顶点的连线AA′,BB′,CC′交于同一点O,且$\frac{AO}{OA′}=\frac{BO}{OB′}=\frac{CO}{OC′}=\frac{2}{3}$.