Question

(本小题满分12分）已知函数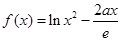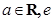，（为自然对数的底数）．

（Ⅰ）求函数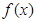的递增区间；

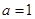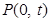
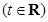（Ⅱ）当时，过点作曲线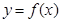的两条切线，设两切点为

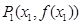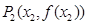
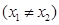，，求证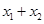为定值，并求出该定值。

 

Answer 1

【答案】

 

解：（Ⅰ）函数的定义域是．

……………………………………………….2分

当时，由，解得；

当时，由，解得；

当时，由，解得，或．-------------4分

所以当时，函数的递增区间是；

当时，函数的递增区间是；

当时，函数的递增区间是，．  …………….6分

（Ⅱ）因为，

所以以为切点的切线的斜率为；

以为切点的切线的斜率为．………………………….8分

又因为切线过点，所以；

…………………………………………..10分

解得， ，. 则.

由已知,从而有． 所以为定值.………………..12分

【解析】略