题目内容
设a，b是正实数，以下不等式其中恒成立的有(1)a+
≥2； (2)
≥a+b； (3)
≥
；（4）a＜|a-b|+b，（ ）
| 1 |
| b |
| 2(a2+b2) |
| ab |
| 2ab |
| a+b |
分析：不妨设a=
，b=1，可得（1）不成立．利用基本不等式可得（2）、（3）正确．不妨设a=5，b=4，可得（4）不正确，由此得出结论．
| 1 |
| 2 |
解答：解：∵a，b是正实数，不妨设a=
，b=1，显然不满足(1)a+
≥2，故（1）不成立．
∵
≥
=|a+b|=a+b，故（2）成立．
∵a，b是正实数，∴a+b≥2
，∴
≤
=
，故（3）正确．
∵a，b是正实数，不妨设a=5，b=4，显然不满足 a＜|a-b|+b，故（4）不正确．
故选B．
| 1 |
| 2 |
| 1 |
| b |
∵
| 2(a2+b2) |
| a2+b2+2ab |
∵a，b是正实数，∴a+b≥2
| ab |
| 2ab |
| a+b |
| 2ab | ||
2
|
| ab |
∵a，b是正实数，不妨设a=5，b=4，显然不满足 a＜|a-b|+b，故（4）不正确．
故选B．
点评：本题主要考查基本不等式的应用，注意基本不等式的使用条件，并注意检验等号成立的条件，利用特殊值代入法，排除不符合条件的选项，是一种简单有效的方法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
（选做题）本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，若多做，则按作答的前两题评分，解答时应写出文字说明、证明过程或演算步骤．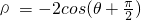
，
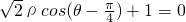，则曲线C1上的点与曲线C2上的点的最远距离为________．
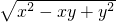，b=p
，c=x+y，若对任意的正实数x，y，都存在以a，b，c为三边长的三角形，则实数p的取值范围是________．
（t为参数），求直线l被曲线C截得的线段长度．
．
（t为参数），求直线l被曲线C截得的线段长度．
．
，
，则曲线C1上的点与曲线C2上的点的最远距离为 ．
，b=p
，c=x+y，若对任意的正实数x，y，都存在以a，b，c为三边长的三角形，则实数p的取值范围是 ．