题目内容
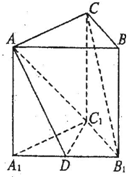 如图,直三棱柱ABC-A1B1C1的底面是等腰直角三角形(侧棱垂直于底面的三棱柱叫做直三棱柱),∠A1C1B1=90o,A1C1=1,AA1=
如图,直三棱柱ABC-A1B1C1的底面是等腰直角三角形(侧棱垂直于底面的三棱柱叫做直三棱柱),∠A1C1B1=90o,A1C1=1,AA1=| 3 |
(1)证明:平面AC1D⊥平面A1B1BA;
(2)证明:B1C∥平面A C1D;
(3)求棱柱ABC-A1B1C1被平面AC1D分成的两部分的体积之比.
分析:(1)在等腰Rt△A1B1C1中利用三线合一,证出C1D⊥A1B1,再根据直三棱柱ABC-A1B1C1中,平面A1B1C1⊥平面A1B1BA,结合面面垂直的性质,得到C1D⊥平面A1B1BA,最后利用线面垂直的判定,可得平面AC1D⊥平面A1B1BA;
(2)利用三角形的中位线定理得到DM∥B1C,再结合线面平行的判定定理可得到B1C∥平面A C1D;
(3)利用棱柱ABC-A1B1C1与三棱锥A-A1C1D有相同的高,结合Rt△A1B1C1中S△A1C1D=
S△A1B1C1,不难算出三棱锥A-A1C1D与棱柱ABC-A1B1C1的体积之比为
,从而得到棱柱ABC-A1B1C1被平面AC1D分成的两部分的体积之比.
(2)利用三角形的中位线定理得到DM∥B1C,再结合线面平行的判定定理可得到B1C∥平面A C1D;
(3)利用棱柱ABC-A1B1C1与三棱锥A-A1C1D有相同的高,结合Rt△A1B1C1中S△A1C1D=
| 1 |
| 2 |
| 1 |
| 6 |
解答:解:(1)∵△A1B1C1是等腰直角三角形,∠A1C1B1=90°且D是线段A1B1的中点
∴C1D⊥A1B1
∵三棱柱ABC-A1B1C1是直三棱柱
∴平面A1B1C1⊥平面A1B1BA
又∵平面A1B1C1与平面A1B1BA的交线为A1B1
∴C1D⊥平面A1B1BA …(3分)
又C1D?平面AC1D …(4分),
∴平面AC1D⊥平面A1B1BA …(5分)
(2)连接A1C,交AC1于M,连接DM,则
∵直三棱柱ABC-A1B1C1中,AA1C1C是矩形 …(6分)
∴M是A1C的中点,
∴△A1B1C中,DM是中位线,可得DM∥B1C …(7分)
又DM?平面AC1D B1C?平面AC1D …(8分)
∴B1C∥平面AC1D …(9分)
(3)由(1)得,在Rt△A1B1C1中,A1C1=B1C1=1,D为A1B1中点
∴S△A1C1D=
S△A1B1C1=
(
×1×1)=
…(11分)
∵直三棱柱ABC-A1B1C1中,A1A⊥平面A1B1C1
∴AA1=
是三棱锥A-A1C1D的高,也是直三棱柱ABC-A1B1C1的高 …(12分)
∴
=
=
=
…(13分)
∴棱柱ABC-A1B1C1被平面AC1D分成的两部分的体积之比为
…(14分)

∴C1D⊥A1B1
∵三棱柱ABC-A1B1C1是直三棱柱
∴平面A1B1C1⊥平面A1B1BA
又∵平面A1B1C1与平面A1B1BA的交线为A1B1
∴C1D⊥平面A1B1BA …(3分)
又C1D?平面AC1D …(4分),
∴平面AC1D⊥平面A1B1BA …(5分)
(2)连接A1C,交AC1于M,连接DM,则
∵直三棱柱ABC-A1B1C1中,AA1C1C是矩形 …(6分)
∴M是A1C的中点,
∴△A1B1C中,DM是中位线,可得DM∥B1C …(7分)
又DM?平面AC1D B1C?平面AC1D …(8分)
∴B1C∥平面AC1D …(9分)
(3)由(1)得,在Rt△A1B1C1中,A1C1=B1C1=1,D为A1B1中点
∴S△A1C1D=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∵直三棱柱ABC-A1B1C1中,A1A⊥平面A1B1C1
∴AA1=
| 3 |
∴
| V三棱锥A-A1C1D |
| V三棱柱ABC-A1B1C1 |
| ||
| S△A1B1C1•AA1 |
| ||||||
|
| 1 |
| 6 |
∴棱柱ABC-A1B1C1被平面AC1D分成的两部分的体积之比为
| 1 |
| 5 |
点评:本题给出一个特殊的直三棱柱,要我们证明线面平行和面面垂直,并求体积的比,着重考查了空间平行、垂直位置关系的证明,属于中档题.

练习册系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.