题目内容
设定义域为R的函数f(x)满足下列条件:①对任意x∈R,f(x)+f(-x)=0;②对任意x∈[-1,1],都有 ,且f(-1)=-1.若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,则当a∈[-1,1]时,t的取值范围是
,且f(-1)=-1.若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,则当a∈[-1,1]时,t的取值范围是
- A.-2≤t≤2
- B.t≤
 或t=0或t≥
或t=0或t≥
- C.-
 ≤t≤
≤t≤
- D.t≤-2或t=0或t≥2
D
分析:由①②和奇函数的定义、增函数的定义,判断出是奇函数、增函数,再求出f(x)在[-1,1]上的最大值,将恒成立转化为:t2-2at≥0对所有的a∈[-1,1]都成立,设g(a)=t2-2at,由一次函数的性质列出不等式求解.
解答:由f(x)+f(-x)=0得,f(x)=-f(-x),
则定义域为R的函数f(x)是奇函数,
∵对任意x∈[-1,1],都有 ,
,
∴f(x)在[-1,1]上是增函数,
则f(x)在[-1,1]上的最大值是f(1)=-f(-1)=1,
∵f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,
∴t2-2at≥0对所有的a∈[-1,1]都成立,
设g(a)=t2-2at,a∈[-1,1],
则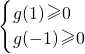 ,∴
,∴ ,解得t≤-2或t=0或t≥2,
,解得t≤-2或t=0或t≥2,
故选D.
点评:本题考查了函数的奇偶性和单调性的综合应用,以及构造函数法解决恒成立问题.
分析:由①②和奇函数的定义、增函数的定义,判断出是奇函数、增函数,再求出f(x)在[-1,1]上的最大值,将恒成立转化为:t2-2at≥0对所有的a∈[-1,1]都成立,设g(a)=t2-2at,由一次函数的性质列出不等式求解.
解答:由f(x)+f(-x)=0得,f(x)=-f(-x),
则定义域为R的函数f(x)是奇函数,
∵对任意x∈[-1,1],都有
 ,
,∴f(x)在[-1,1]上是增函数,
则f(x)在[-1,1]上的最大值是f(1)=-f(-1)=1,
∵f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,
∴t2-2at≥0对所有的a∈[-1,1]都成立,
设g(a)=t2-2at,a∈[-1,1],
则
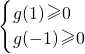 ,∴
,∴ ,解得t≤-2或t=0或t≥2,
,解得t≤-2或t=0或t≥2,故选D.
点评:本题考查了函数的奇偶性和单调性的综合应用,以及构造函数法解决恒成立问题.

练习册系列答案
相关题目