题目内容
【题目】在正方体![]() 中,点E是棱
中,点E是棱![]() 的中点,点F是线段
的中点,点F是线段![]() 上的一个动点.有以下三个命题:
上的一个动点.有以下三个命题:
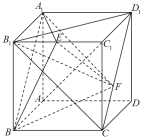
①异面直线![]() 与
与![]() 所成的角是定值;
所成的角是定值;
②三棱锥![]() 的体积是定值;
的体积是定值;
③直线![]() 与平面
与平面![]() 所成的角是定值.
所成的角是定值.
其中真命题的个数是( )
A. 3 B. 2 C. 1 D. 0
【答案】B
【解析】
以A点为坐标原点,AB,AD,![]() 所在直线为x轴,y轴,z轴建立空间直角坐标系,
所在直线为x轴,y轴,z轴建立空间直角坐标系,
可得![]() =(1,1,1),
=(1,1,1),![]() =(t-1,1,-t),可得
=(t-1,1,-t),可得![]() =0,可得①正确;
=0,可得①正确;
由三棱锥![]() 的底面
的底面![]() 面积为定值,且
面积为定值,且![]() ∥
∥![]() ,可得②正确;
,可得②正确;
可得![]() =(t,1,-t),平面
=(t,1,-t),平面![]() 的一个法向量为
的一个法向量为![]() =(1,1,1),可得
=(1,1,1),可得![]() 不为定值可得③错误,可得答案.
不为定值可得③错误,可得答案.
解:以A点为坐标原点,AB,AD,![]() 所在直线为x轴,y轴,z轴建立空间直角坐标系,设正方体棱长为1,可得B(1,0,0),C(1,1,O),D(0,1,0),
所在直线为x轴,y轴,z轴建立空间直角坐标系,设正方体棱长为1,可得B(1,0,0),C(1,1,O),D(0,1,0),![]() (0,0,1),
(0,0,1),![]() (1,0,1),
(1,0,1),![]() (1,1,1),
(1,1,1),![]() (0,1,1),设F(t,1,1-t),(0≤t≤1),
(0,1,1),设F(t,1,1-t),(0≤t≤1),
可得![]() =(1,1,1),
=(1,1,1),![]() =(t-1,1,-t),可得
=(t-1,1,-t),可得![]() =0,故异面直线
=0,故异面直线![]() 与
与![]() 所的角是定值,故①正确;
所的角是定值,故①正确;
三棱锥![]() 的底面
的底面![]() 面积为定值,且
面积为定值,且![]() ∥
∥![]() ,点F是线段
,点F是线段![]() 上的一个动点,可得F点到底面
上的一个动点,可得F点到底面![]() 的距离为定值,故三棱锥
的距离为定值,故三棱锥![]() 的体积是定值,故②正确;
的体积是定值,故②正确;
可得![]() =(t,1,-t),
=(t,1,-t),![]() =(0,1,-1),
=(0,1,-1),![]() =(-1,1,0),可得平面
=(-1,1,0),可得平面![]() 的一个法向量为
的一个法向量为![]() =(1,1,1),可得
=(1,1,1),可得![]() 不为定值,故③错误;
不为定值,故③错误;
故选B.

练习册系列答案
相关题目