题目内容
已知函数f(x)=
解:∵f(2)=1,∴1=![]() ,即2a+b=2. ①
,即2a+b=2. ①
又∵f(x)=x有唯一解,即![]() =x有唯一解,∴x·
=x有唯一解,∴x·![]() =0.
=0.
解之,得x1=0,x2=![]() ,
,
∵有唯一的解,∴x1=x2=0,得b=1. ②
由①②得a=![]() ,b=1.
,b=1.
∴f(x)=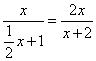 .
.
故f[f(-3)]=f(![]() )=f(6)=
)=f(6)= ![]() .
.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|