Question

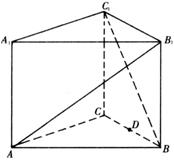
正三棱柱ABC-A₁B₁C₁中，D是BC的中点，AB=BB₁=a．

(1)求点D到平面ACC₁的距离；

(2)判断A₁B与平面ADC₁的位置关系，并证明你的结论；

(3)求异面直线AB₁与C₁B所成的角.

Answer 1

解：(1)取AC的中点E，则BE⊥面ACC₁.

取CE的中点9，则DF∥BE．于是DF⊥面ACC₁，

故DF为D到面ACC₁的距离．

DF=BE=·．

(2)设A₁C与AC₁交于点C，则G是A₁C的中点．

又D是BC的中点，∴GD∥A₁B．

∵GD面AC₁D，∴A₁B∥面AC₁D．

(3)∵AD⊥CB，∴AD⊥平面CBB₁C₁．

故AB₁在面CBB₁C₁上的射影为B₁D．

在矩形CBB₁C₁中，∵，

∴△C₁CB∽DBB₁.

故∠BDB₁+∠DBC₁=，∴DB₁⊥BC₁.

由三垂线定理知，BC₁⊥AB₁，∴BC₁与AB₁所成角为．