题目内容
在教材中,我们学过“经过点P(x,y,z),法向量为 的平面的方程是:A(x-x)+B(y-y)+C(z-z)=0”.现在我们给出平面α的方程是x-y+z=1,平面β的方程是
的平面的方程是:A(x-x)+B(y-y)+C(z-z)=0”.现在我们给出平面α的方程是x-y+z=1,平面β的方程是 ,则由这两平面所成的锐二面角的余弦值是( )
,则由这两平面所成的锐二面角的余弦值是( )A.
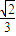
B.

C.
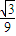
D.
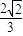
【答案】分析:由定义可得:两个平面的法向量分别为: =(1,-1,1),
=(1,-1,1), =(1,-2,-1),再利用向量的数量积公式可得两个向量的夹角的余弦值,进而根据向量的夹角与二面角的平面角的关系得到答案.
=(1,-2,-1),再利用向量的数量积公式可得两个向量的夹角的余弦值,进而根据向量的夹角与二面角的平面角的关系得到答案.
解答:解:由定义可得:平面x-y+z=1的法向量为 =(1,-1,1),平面
=(1,-1,1),平面 的法向量为
的法向量为 =(1,-2,-1),
=(1,-2,-1),
所以两个向量的夹角余弦值为:cos =
= =
= ,
,
所以平面所成的锐二面角的余弦值 .
.
故选A.
点评:本题主要考查由平面方程求平面的法向量,以及向量的数量积运算求两个向量的夹角,此题属于基础题.
 =(1,-1,1),
=(1,-1,1), =(1,-2,-1),再利用向量的数量积公式可得两个向量的夹角的余弦值,进而根据向量的夹角与二面角的平面角的关系得到答案.
=(1,-2,-1),再利用向量的数量积公式可得两个向量的夹角的余弦值,进而根据向量的夹角与二面角的平面角的关系得到答案.解答:解:由定义可得:平面x-y+z=1的法向量为
 =(1,-1,1),平面
=(1,-1,1),平面 的法向量为
的法向量为 =(1,-2,-1),
=(1,-2,-1),所以两个向量的夹角余弦值为:cos
 =
= =
= ,
,所以平面所成的锐二面角的余弦值
 .
.故选A.
点评:本题主要考查由平面方程求平面的法向量,以及向量的数量积运算求两个向量的夹角,此题属于基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目