Question

【题目】对于曲线（其中为自然对数的底数）上任意一点处的切线，总存在在曲线上一点处的切线，使得∥，则实数的取值范围是____________.

Answer 1

【答案】.

【解析】分析：分别求出两个函数导数函数的值域，进而将已知转化为两个值域存在包含关系，进而可得答案．

详解：∵，∴

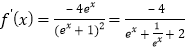
∵,故

∵,∴，

g′′（x）=2（lnx+1），

当x∈（0，）时，g′′（x）＜0，g′（x）为减函数；

当x∈（，+∞）时，g′′（x）＞0，g′（x）为增函数；

故当x=时，g′（x）取最小值a﹣，即g′（x）∈[a﹣，0）

若对于曲线（其中e为自然对数的底数）上任意一点处的切线l1，

总存在在曲线上一点处的切线l2，使得l1∥l2，

则[﹣1，0）[a﹣，0）,即a﹣≤﹣1．

解得：a∈，

故答案为：.