题目内容
【题目】古希腊毕达哥拉斯学派研究了“多边形数”,人们把多边形数推广到空间,研究了“四面体数”,下图是第一至第四个四面体数,(已知![]() )
)
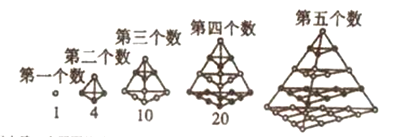
观察上图,由此得出第5个四面体数为______(用数字作答);第![]() 个四面体数为______.
个四面体数为______.
【答案】35 ![]()
【解析】
通过观察图形,先将图形的规律转化为数字规律,即为找到如1,4,10,20,……的数列的第![]() 项,通过观察发现,相邻的数字差分别是3,6,10,……,即第
项,通过观察发现,相邻的数字差分别是3,6,10,……,即第![]() 项应为
项应为![]() ,那么就把问题转化为求数列
,那么就把问题转化为求数列![]() 的和,
的和,![]() 为1,3,6,10,……,根据这些数字可以发现,
为1,3,6,10,……,根据这些数字可以发现,![]() ,
, ![]() ,……,
,……, ![]() ,利用累加法可以得到
,利用累加法可以得到![]() ,再利用题目所给已知,求出前
,再利用题目所给已知,求出前![]() 项和,即为第
项和,即为第![]() 个四面体数,当
个四面体数,当![]() 时,即为第5个四面体数.
时,即为第5个四面体数.
由题,
第一个四面体数为1;
第二个四面体数为![]() ;
;
第三个四面体数为![]() ;
;
第四个四面体数为![]()
……
由此可归纳,第![]() 个四面体数为
个四面体数为![]()
即为![]()
设该式中的每个数从左至右的排列为数列![]() ,即
,即![]() 为:1,3,6,10,……
为:1,3,6,10,……
得到递推关系为![]() ,
,![]() ,…,
,…,![]() ,相加后得
,相加后得![]()
![]() ,故数列
,故数列![]() 的和
的和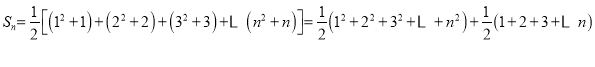
![]()
![]() 当
当![]() 时,
时,![]()
故答案为:35;![]()

练习册系列答案
相关题目
