题目内容
已知函数f(x)=ax2+2ln(x+1),其中a为实数,
(1)若f(x)在x=1处有极值,求a的值;
(2)若f(x)在[2,3]上是增函数,求a的取值范围。
(1)若f(x)在x=1处有极值,求a的值;
(2)若f(x)在[2,3]上是增函数,求a的取值范围。
解:(1)由已知得f(x)的定义域为(-1,+∞),
又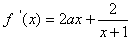 ,
,
∴由题意得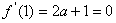 ,
,
∴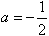 ;
;
(2)依题意得,f′(x)>0对x∈[2,3]恒成立,
∴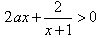 ,
,
∴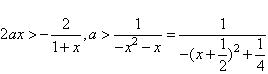 ,
,
∵x∈[2,3],
∴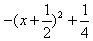 的最小值为
的最小值为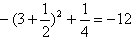 ,
,
∴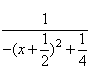 的最大值为
的最大值为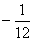 ,
,
又因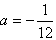 时符合题意,
时符合题意,
∴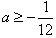 为所求。
为所求。
又
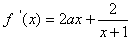 ,
,∴由题意得
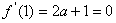 ,
,∴
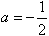 ;
;(2)依题意得,f′(x)>0对x∈[2,3]恒成立,
∴
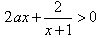 ,
,∴
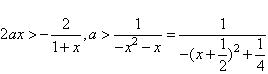 ,
,∵x∈[2,3],
∴
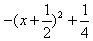 的最小值为
的最小值为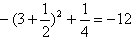 ,
,∴
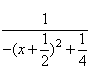 的最大值为
的最大值为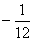 ,
,又因
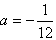 时符合题意,
时符合题意, ∴
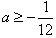 为所求。
为所求。
练习册系列答案
相关题目