Question

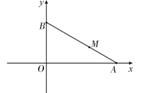
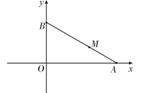
 如图，长为m＋1（m＞0）的线段AB的两个端点A和B分别在x轴和y轴上滑动，点M是线段AB上一点，且．

（1）求点M的轨迹Γ的方程，并判断轨迹Γ为何种圆锥曲线；

（2）设过点Q(，0)且斜率不为0的直线交轨迹Γ于C、D两点．

试问在x轴上是否存在定点P，使PQ平分∠CPD？若存在，求点P的坐标；

若不存在，请说明理由．

Answer 1

 解：（1）设A、B、M的坐标分别为(x₀，0)、(0，y₀)、(x，y)，则

x＋y＝(m＋1)²，                            ①

由＝m，得(x－x₀，y)＝m(－x，y₀－y)，

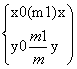∴∴         ②

将②代入①，得

(m＋1)²x²＋()²y²＝(m＋1)²，

化简即得点M的轨迹Γ的方程为x²＋＝1（m＞0）．

当0＜m＜1时，轨迹Γ是焦点在x轴上的椭圆；

当m＝1时，轨迹Γ是以原点为圆心，半径为1的圆；

当m＞1时，轨迹Γ是焦点在y轴上的椭圆．

（2）依题意，设直线CD的方程为x＝ty＋，

由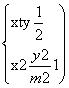消去x并化简整理，得(m²t²＋1)y²＋m²ty－m²＝0，

△＝m⁴t²＋3m²(m²t²＋1)＞0，

设C(x₁，y₁)，D(x₂，y₂)，则

y₁＋y₂＝－，y₁y₂＝－．         ③

假设在x轴上存在定点P(a，0)，使PQ平分∠CPD，

则直线PC、PD的倾斜角互补，

∴k_PC＋k_PD＝0，即＋＝0，

∵x₁＝ty₁＋，x₂＝ty₂＋，∴＋＝0，

化简，得4ty₁y₂＋(1－2a)( y₁＋y₂)＝0．           ④

将③代入④，得－－＝0，即－2m²t(2－a)＝0，

∵m＞0，∴t(2－a)＝0，∵上式对∀t∈R都成立，∴a＝2．

故在x轴上存在定点P(2，0)，使PQ平分∠CPD．