Question

【题目】已知函数， .

(1)讨论函数的单调性；

(2)已知，若函数恒成立，试确定的取值范围.

Answer 1

【答案】(1)答案见解析；(2) .

【解析】试题分析：

(1)由函数的解析式有，结合二次函数的性质分类讨论：

当时，函数在上单调递增；

当时， 在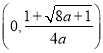上单调递增，在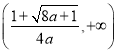上单调递减.

(2)由(1)可知， ，满足题意时需，即，结合题意构造函数在，结合函数的性质可得的取值范围是.

试题解析：

(1)由，得： ， ，

当时， 在上恒成立，函数在上单调递增；

当时，令，则，得， ，

∵，∴，

∴令得，令得，

∴在上单调递增，在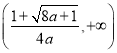上单调递减.

(2)由(1)可知，当时，函数在上单调递增，在上单调递减，

∴，

即需，即，

又由得，代入上面的不等式得，

由函数在上单调递增， ，

所以，∴，∴，

所以的取值范围是.