题目内容
用数学归纳法证明
![]()
(1)当![]() 时,左边
时,左边![]()
右边![]() ,等式成立.
,等式成立.
(2)假设当![]() 时,
时,![]() 等式成立,即
等式成立,即
![]()
则当![]() 时,
时,
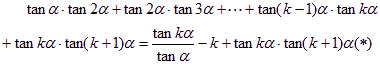
由![]() 得
得![]()
代入![]() 式,得
式,得
右边![]()
即![]()
![]()
这就是说,当![]() 时等式成立.
时等式成立.
根据(1)、(2)可知,对任意![]() ,等式成立
,等式成立
解析:
在由假设![]() 时等式成立,推导当
时等式成立,推导当![]() 时等式成立时,要灵活应用三角公式及其变形公式,本题中涉及到两个角的正切的乘积问题,联想到两角差的正切公式的变形公式:
时等式成立时,要灵活应用三角公式及其变形公式,本题中涉及到两个角的正切的乘积问题,联想到两角差的正切公式的变形公式:![]() ,问题就会迎刃而解
,问题就会迎刃而解

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目