题目内容
函数f(x)=lnx- 在区间(k,k+1)(k∈N*)上存在零点,则k的值为
在区间(k,k+1)(k∈N*)上存在零点,则k的值为
- A.0
- B.2
- C.0或2
- D.1或2
C
分析:利用导数求得函数f(x)在区间(0,1),及(1,+∞)都是单调增的,再根据 f( )<0,f(
)<0,f( )>0,可得 f(
)>0,可得 f( )f(
)f( )<0,故函数f(x)在区间
)<0,故函数f(x)在区间
( ,
, )上有一个零点,故函数f(x)在区间(0,1)上有一个零点,故k=0满足条件.
)上有一个零点,故函数f(x)在区间(0,1)上有一个零点,故k=0满足条件.
同理由 f(2)f(3)<0,可得函数在(2,3)上存在1个零点,故k=2满足条件,综合可得结论.
解答:由函数的解析式可得函数的定义域为{x|x>0 且x≠1},求得函数的导数f′(x)= +
+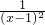 在它的定义域内为正实数,
在它的定义域内为正实数,
故函数f(x)在区间(0,1),及(1,+∞)都是单调递增的,
再根据 f( )=-2-
)=-2-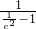 =-2+
=-2+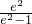 =-2+
=-2+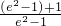 =-1+
=-1+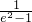 <0,f(
<0,f( )=-1+
)=-1+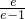 =-1+
=-1+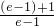 =
=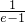 >0,
>0,
可得 f( )f(
)f( )<0,故函数f(x)在区间(
)<0,故函数f(x)在区间(
 )上有一个零点,故函数f(x)在区间(0,1)上有一个零点,故k=0满足条件.
)上有一个零点,故函数f(x)在区间(0,1)上有一个零点,故k=0满足条件.
再由 f(2)=ln2-1<0,f(3)=ln3- >0,f(2)f(3)<0,可得函数在(2,3)上存在1个零点,故k=2满足条件.
>0,f(2)f(3)<0,可得函数在(2,3)上存在1个零点,故k=2满足条件.
故选 C.
点评:本题主要考查利用导数研究函数的单调性,函数零点的判定定理的应用,属于基础题
分析:利用导数求得函数f(x)在区间(0,1),及(1,+∞)都是单调增的,再根据 f(
 )<0,f(
)<0,f( )>0,可得 f(
)>0,可得 f( )f(
)f( )<0,故函数f(x)在区间
)<0,故函数f(x)在区间(
 ,
, )上有一个零点,故函数f(x)在区间(0,1)上有一个零点,故k=0满足条件.
)上有一个零点,故函数f(x)在区间(0,1)上有一个零点,故k=0满足条件.同理由 f(2)f(3)<0,可得函数在(2,3)上存在1个零点,故k=2满足条件,综合可得结论.
解答:由函数的解析式可得函数的定义域为{x|x>0 且x≠1},求得函数的导数f′(x)=
 +
+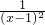 在它的定义域内为正实数,
在它的定义域内为正实数,故函数f(x)在区间(0,1),及(1,+∞)都是单调递增的,
再根据 f(
 )=-2-
)=-2-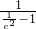 =-2+
=-2+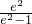 =-2+
=-2+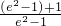 =-1+
=-1+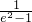 <0,f(
<0,f( )=-1+
)=-1+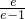 =-1+
=-1+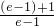 =
=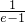 >0,
>0,可得 f(
 )f(
)f( )<0,故函数f(x)在区间(
)<0,故函数f(x)在区间(
 )上有一个零点,故函数f(x)在区间(0,1)上有一个零点,故k=0满足条件.
)上有一个零点,故函数f(x)在区间(0,1)上有一个零点,故k=0满足条件.再由 f(2)=ln2-1<0,f(3)=ln3-
 >0,f(2)f(3)<0,可得函数在(2,3)上存在1个零点,故k=2满足条件.
>0,f(2)f(3)<0,可得函数在(2,3)上存在1个零点,故k=2满足条件.故选 C.
点评:本题主要考查利用导数研究函数的单调性,函数零点的判定定理的应用,属于基础题

练习册系列答案
相关题目