题目内容
已知函数 ,其中a>0且a≠1.
,其中a>0且a≠1.
(1)分别判断f(x)在(-∞,+∞)上的单调性;
(2)比较f(1)-1与f(2)-2、f(2)-2与f(3)-3的大小,由此归纳出一个更一般的结论,并证明;
(3)比较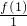 与
与 、
、 与
与 的大小,由此归纳出一个更一般的结论,并证明.
的大小,由此归纳出一个更一般的结论,并证明.
解:(1)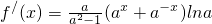 ,
,
若0<a<1,则 ,lna<0,所以f/(x)>0;
,lna<0,所以f/(x)>0;
若a>1,则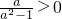 ,lna>0,所以f/(x)>0,
,lna>0,所以f/(x)>0,
因此,任意a>0且a≠1,都有f/(x)>0,f(x)在(-∞,+∞)上的单调递增.
(2)直接计算知f(1)-1=0,f(2)-2=a+a-1-2,f(3)-3=a2+a-2-2,
根据基本不等式a+a-1-2>0,所以f(2)-2>f(1)-1,
又因为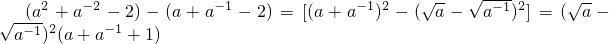 =
=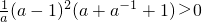 ,
,
所以f(3)-3>f(2)-2.
假设?x>0,f(x+1)-(x+1)>f(x)-x.
记g(x)=[f(x+1)-(x+1)]-[f(x)-x]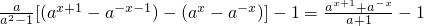 ,
,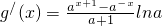 .与(1)类似地讨论知,对?x>0和?a>0且a≠1都有g/(x)>0,g(x)在[0,+∞)上的单调递增,g(0)=0,
.与(1)类似地讨论知,对?x>0和?a>0且a≠1都有g/(x)>0,g(x)在[0,+∞)上的单调递增,g(0)=0,
所以g(x)>g(0)=0,即?x>0,f(x+1)-(x+1)>f(x)-x.
(3) ,
, ,
, ,
,
根据基本不等式 ,
, ,
,
所以 .
.
假设?x>0, .
.
记 ,x>0,
,x>0,
 ,
,
设 ,
,
则h(0)=0且 ,
,
类似(1)的讨论知 ,
,
从而h(x)>h(0)=0,g/(x)>0,g(x)在R+上单调增加,
所以?x>0, .
.
分析:(1)先求导,再判导数的符号.
(2)直接计算f(1)-1与f(2)-2、f(2)-2与f(3)-3,进行比较.比较大小可用做差比较法.
归纳一般的结论,构造函数利用单调性进行证明.
(3)利用基本不等式和做差比较法比较大小,归纳结论,构造函数进行证明.
点评:本题考查比较大小、归纳推理、函数单调性的证明及应用,综合性强,难度较大.
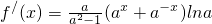 ,
,若0<a<1,则
 ,lna<0,所以f/(x)>0;
,lna<0,所以f/(x)>0;若a>1,则
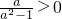 ,lna>0,所以f/(x)>0,
,lna>0,所以f/(x)>0,因此,任意a>0且a≠1,都有f/(x)>0,f(x)在(-∞,+∞)上的单调递增.
(2)直接计算知f(1)-1=0,f(2)-2=a+a-1-2,f(3)-3=a2+a-2-2,
根据基本不等式a+a-1-2>0,所以f(2)-2>f(1)-1,
又因为
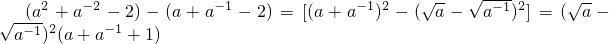 =
=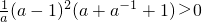 ,
,所以f(3)-3>f(2)-2.
假设?x>0,f(x+1)-(x+1)>f(x)-x.
记g(x)=[f(x+1)-(x+1)]-[f(x)-x]
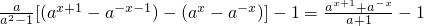 ,
,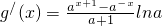 .与(1)类似地讨论知,对?x>0和?a>0且a≠1都有g/(x)>0,g(x)在[0,+∞)上的单调递增,g(0)=0,
.与(1)类似地讨论知,对?x>0和?a>0且a≠1都有g/(x)>0,g(x)在[0,+∞)上的单调递增,g(0)=0,所以g(x)>g(0)=0,即?x>0,f(x+1)-(x+1)>f(x)-x.
(3)
 ,
, ,
, ,
,根据基本不等式
 ,
, ,
,所以
 .
.假设?x>0,
 .
.记
 ,x>0,
,x>0,
 ,
,设
 ,
,则h(0)=0且
 ,
,类似(1)的讨论知
 ,
,从而h(x)>h(0)=0,g/(x)>0,g(x)在R+上单调增加,
所以?x>0,
 .
.分析:(1)先求导,再判导数的符号.
(2)直接计算f(1)-1与f(2)-2、f(2)-2与f(3)-3,进行比较.比较大小可用做差比较法.
归纳一般的结论,构造函数利用单调性进行证明.
(3)利用基本不等式和做差比较法比较大小,归纳结论,构造函数进行证明.
点评:本题考查比较大小、归纳推理、函数单调性的证明及应用,综合性强,难度较大.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 ,其中a>0.
,其中a>0. ,其中a>0.
,其中a>0.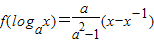 ,其中a>0且a≠1.
,其中a>0且a≠1.