Question

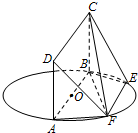如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面与圆O所在的平面互相垂直．已知AB=2，EF=1．
（Ⅰ）求证：平面DAF⊥平面CBF；
（Ⅱ）求直线AB与平面CBF所成角的大小；
（Ⅲ）当AD的长为何值时，平面DFC与平面FCB所成的锐二面角的大小为60°？

Answer 1

分析：（I）利用面面垂直的性质，可得CB⊥平面ABEF，再利用线面垂直的判定，证明AF⊥平面CBF，从而利用面面垂直的判定可得平面DAF⊥平面CBF；
（II）确定∠ABF为直线AB与平面CBF所成的角，过点F作FH⊥AB，交AB于H，计算出AF，即可求得直线AB与平面CBF所成角的大小；
（Ⅲ）建立空间直角坐标系，求出平面DCF的法向量

n1

=(0， 2t， 

3

)，平面CBF的一个法向量

n2

=

AF

=(-

1

2

， 

3

2

， 0)，利用向量的夹角公式，即可求得AD的长．

解答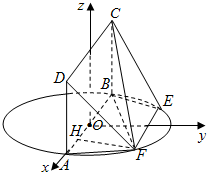：（I）证明：∵平面ABCD⊥平面ABEF，CB⊥AB，平面ABCD∩平面ABEF=AB，
∴CB⊥平面ABEF．
∵AF?平面ABEF，∴AF⊥CB，…（2分）
又∵AB为圆O的直径，∴AF⊥BF，∴AF⊥平面CBF．         …（3分）
∵AF?平面ADF，∴平面DAF⊥平面CBF．…（4分）
（II）解：根据（Ⅰ）的证明，有AF⊥平面CBF，
∴FB为AB在平面CBF内的射影，因此，∠ABF为直线AB与平面CBF所成的角                   …（6分）
∵AB∥EF，∴四边形ABEF为等腰梯形，
过点F作FH⊥AB，交AB于H．
AB=2，EF=1，则AH=

AB-EF

2

=

1

2

．
在Rt△AFB中，根据射影定理AF²=AH•AB，得AF=1．       …（8分）
∴sin∠ABF=

AF

AB

=

1

2

，∴∠ABF=30°．
∴直线AB与平面CBF所成角的大小为30°．                         …（9分）
（Ⅲ）解：设EF中点为G，以O为坐标原点，OA、OG、AD方向分别为x轴、y轴、z轴方向建立空间直角坐标系（如图）．
设AD=t（t＞0），则点D的坐标为（1，0，t），则 C（-1，0，t），A(1，0，0)，B(-1，0，0)，F(

1

2

，

3

2

，0)
∴

CD

=(2，0，0)，

FD

=(

1

2

，-

3

2

，t)…（10分）
设平面DCF的法向量为

n1

=(x，y，z)，则

n1

•

CD

=0，

n1

•

FD

=0，即

2x=0 - 3 2 y+tz=0.

令z=

3

，解得x=0，y=2t，∴

n1

=(0， 2t， 

3

)…（12分）
由（I）可知AF⊥平面CFB，取平面CBF的一个法向量为

n2

=

AF

=(-

1

2

， 

3

2

， 0)，
依题意

n1

与

n2

的夹角为60°，∴cos60°=

n1 • n2

| n1 |•| n2 |

，即

1

2

=

3 t

4t2+3 •1

，解得t=

6

4

因此，当AD的长为

6

4

时，平面与DFC平面FCB所成的锐二面角的大小为60°．…（14分）

点评：本题考查面面垂直，考查线面角，考查面面角，考查向量知识的运用，考查学生分析解决问题的能力，求出平面的法向量是关键．