Question

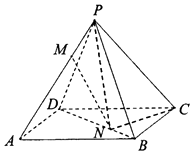
【题目】如图所示，已知长方体ABCD中， 为DC的中点．将△ADM沿AM折起，使得AD⊥BM．
（1）求证：平面ADM⊥平面ABCM；
（2）是否存在满足 的点E，使得二面角E﹣AM﹣D为大小为 ．若存在，求出相应的实数t；若不存在，请说明理由．

Answer 1

【答案】
（1）证明：∵长方形ABCD中，AB=2AD=2 ，M为DC的中点，

∴AM=BM=2，AM2+BM2=AB2，∴BM⊥AM，

∵AD⊥BM，AD∩AM=A，∴BM⊥平面ADM，

又BM平面ABCM，∴平面ADM⊥平面ABCM

（2）解：以M为原点，MA为x轴，MB为y轴，过M作平面ABCM的垂线为z轴，

建立空间直角坐标系，

则A（2，0，0），B（0，2，0），D（1，0，1），M（0，0，0），

=（0，2，0）， =（1，﹣2，1）， = =（t，2﹣2t，1），

设平面AME的一个法向量为 =（x，y，z），

则 ，

取y=t，得 =（0，t，2t﹣2），

由（1）知平面AMD的一个法向量 =（0，1，0），

∵二面角E﹣AM﹣D为大小为 ，

∴cos = = = ，

解得t= 或t=2（舍），

∴存在满足 的点E，使得二面角E﹣AM﹣D为大小为 ，相应的实数t的值为 ．

【解析】（1）推导出BM⊥AM，AD⊥BM，从而BM⊥平面ADM，由此能证明平面ADM⊥平面ABCM．（2）以M为原点，MA为x轴，MB为y轴，过M作平面ABCM的垂线为z轴，建立空间直角坐标系，利用向量法能求出存在满足 的点E，使得二面角E﹣AM﹣D为大小为 ，并能求出相应的实数t的值．
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案，需要熟知一个平面过另一个平面的垂线，则这两个平面垂直．