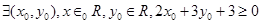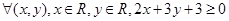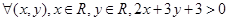题目内容
设命题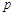 :函数
:函数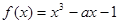 在区间
在区间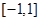 上单调递减;命题
上单调递减;命题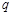 :函数
:函数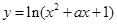 的定义域是
的定义域是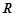 .如果命题
.如果命题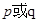 为真命题,
为真命题,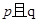 为假命题,求
为假命题,求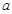 的取值范围.
的取值范围.
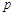 :函数
:函数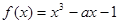 在区间
在区间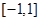 上单调递减;命题
上单调递减;命题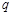 :函数
:函数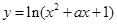 的定义域是
的定义域是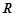 .如果命题
.如果命题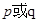 为真命题,
为真命题,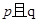 为假命题,求
为假命题,求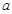 的取值范围.
的取值范围.
由题意命题p或q为真命题,p且q为假命题,可知p、q一真一假.
然后分别求出p,q为真的条件,再分p真q假和p假q真两种情况分别求出a的值,再求并集即可.
解:p为真命题
 在
在 上恒成立
上恒成立

 在
在 上恒成立
上恒成立


q为真命题
 恒成立
恒成立


由题意p和q有且只有一个是真命题
p真q假

p假q真

综上所述:a的范围是
然后分别求出p,q为真的条件,再分p真q假和p假q真两种情况分别求出a的值,再求并集即可.
解:p为真命题

 在
在 上恒成立
上恒成立
 在
在 上恒成立
上恒成立

q为真命题

 恒成立
恒成立

由题意p和q有且只有一个是真命题
p真q假


p假q真


综上所述:a的范围是


练习册系列答案
相关题目
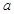 、
、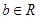 ,若
,若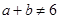 ,则
,则 ”是一个真命题
”是一个真命题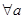 、
、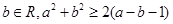 ”的否定是:“
”的否定是:“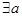 、
、 ”
”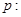 对于
对于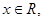 恒有
恒有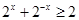 成立;命题
成立;命题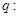 奇函数
奇函数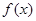 的图像必过原点,则下列结论正确的是( )
的图像必过原点,则下列结论正确的是( )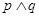 为真
为真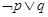 为真
为真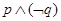 为真
为真 为真
为真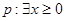 ,
,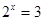 ,则( )
,则( )  ,
,
 ,
, ,
, ,
,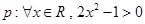 ,则该命题的否定是 。
,则该命题的否定是 。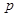 :若
:若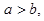 则
则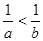 ;
;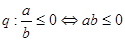 .给出下列四个复合命题:①
.给出下列四个复合命题:① ,②
,②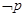 ,④
,④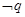 .其中真命题有( )
.其中真命题有( )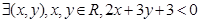 ”的否定是
”的否定是 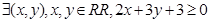
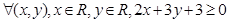

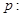 “
“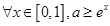 ”,命题
”,命题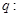 “
“ ”,若
”,若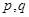 均是真命题,则实数
均是真命题,则实数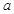 的取值范围是( )
的取值范围是( )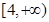
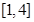
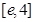
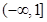
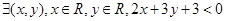 ”的否定是( )
”的否定是( )