Question

设集合A={x|x²+4x≤0}，B={x|x²+ax+a≤0}，若A∪B=A，求实数a的取值范围.

Answer 1

思路解析:由于集合A是已知的,所以要先化简集合A，根据已知条件A∪B=A,集合B可能是空集也可能不是空集,所以要对集合B进行分类，这一点要特别注意,再进一步求出a的取值范围.

解：A={x|-4≤x≤0}.

∵A∪B=A,∴BA.

1°当B=时,Δ=a²-4a＜0,

∴0＜a＜4.

2°当B≠时，Δ=a²-4a≥0，

∴a≤0或a≥4.

令f(x)=x²+ax+a，要使BA，即要求f(x)与x轴的交点在［-4，0］上,

∴

∴

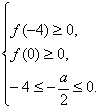
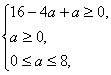
∴0≤a≤.

综合1°,2°实数a的取值范围为［0,］.