题目内容
已知正方体ABCD-A1B1C1D1中，点E，F分别是棱AB，AA1的中点，求证：三条直线DA，CE，D1F交于一点。
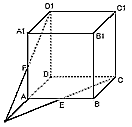
证明：连结EF、
、
，
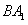在正方体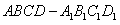
中，点E、F分别是棱
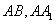的中点，
∴
，
，
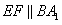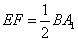又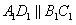
，
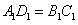
∴四边形A1BCD1为平行四边形，
∴
，
，
∴
，
，
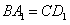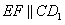∴四边形是梯形，
∴
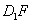与CE的延长线交于一个点，设为O点，则有O∈
，
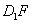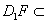平面AD1，
∴O∈平面AD1，同理O∈平面AC，且平面AD1∩平面AC=AD，
∴O∈AD，
∴三条直线
交于一点。
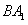、，在正方体
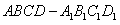中，点E、F分别是棱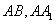的中点，∴
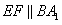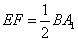，，又
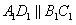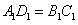
，∴四边形A1BCD1为平行四边形，
∴
，，∴
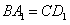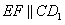，，∴四边形是梯形，
∴
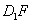与CE的延长线交于一个点，设为O点，则有O∈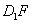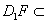，平面AD1，∴O∈平面AD1，同理O∈平面AC，且平面AD1∩平面AC=AD，
∴O∈AD，
∴三条直线
交于一点。 
练习册系列答案
阅读快车系列答案
相关题目
如图，已知正方体ABCD-A1B1C1D1的棱长为2，点P在平面DD1C1C内，PD1=PC1=
已知正方体ABCD-A1B1C1D1，O是底ABCD对角线的交点．