��Ŀ����
1��ij����ͣ������ʱͣ����ʱ���շѣ��շѱ�Ϊ��ÿ������һ��ͣ��������1Сʱ�շ�6Ԫ������1Сʱ�IJ���ÿСʱ�շ�8Ԫ������1Сʱ�IJ��ְ�1Сʱ���㣩�����мס��Ҷ����ڸ�������ʱͣ��������ͣ����������4Сʱ���������ͣ������aԪ���������⣬��д�±���
| ��ͣ��ʱ�� ��Сʱ�� | ��0��1] | ��1��2] | ��2��3] | ��3��4] |
| ��ͣ����a ��Ԫ�� |
��������ͣ��1Сʱ�����Ҳ�����2Сʱ�ĸ���Ϊ$\frac{1}{3}$��ͣ�����Ѷ���14Ԫ�ĸ���Ϊ$\frac{5}{12}$�����ͣ������ǡΪ6Ԫ�ĸ��ʣ�
���� ����������ɵñ���
����ͣ������aԪ������ͣ������bԪ������a��b=6��14��22��30���оٿɵ��ܵĻ����¼����ɸ��ʹ�ʽ�ɵã�
�����ɶ����¼��ĸ��ʹ�ʽ�ɵã�
��� �⣺����������ɵñ������£�
| ��ͣ��ʱ�� ��Сʱ�� | ��0��1] | ��1��2] | ��2��3] | ��3��4] |
| ��ͣ����a ��Ԫ�� | 6 | 14 | 22 | 30 |
��ס��Ҷ��˵�ͣ�����ù��ɵĻ����¼��ռ�Ϊ����6��6������6��14������6��22����
��6��30������14��6������14��14������14��22������14��30������22��6������22��14����
��22��22������22��30������30��6������30��14������30��22������30��30������16������
���У�6��30������14��22������22��14������30��6����4�����η������⣮
�ʡ��ס��Ҷ���ͣ������֮��Ϊ36Ԫ���ĸ���Ϊ$P=\frac{4}{16}=\frac{1}{4}$��
��������ʱͣ������ǡΪ6Ԫ��Ϊ�¼�A��
�� $P��A��=1-��\frac{1}{3}+\frac{5}{12}��=\frac{1}{4}$��
�����ʱͣ������ǡΪ6Ԫ�ĸ�����$\frac{1}{4}$
���� ���⿼��ŵ���ͼ�����ʹ�ʽ���о��ǽ������Ĺؼ����������⣮

��ϰ��ϵ�д�
�����Ŀ
9����������㷨��˵����ȷ���ǣ�������
| A�� | �ؾ����㷨���������������Լ���ķ��� | |
| B�� | ����������������ʽ��ֵ�ķ��� | |
| C�� | ��Բ���Dz��������������ƽ�Բ������㷨����Բ���ʦ� | |
| D�� | ���Ͻ��۽Դ� |
6����֪f�䣨x�����溯��f��x���ĵ�������f��-1��=0����x��0ʱ��xf�䣨x��+f��x����0����ʹ��f��x����0������x��ȡֵ��Χ�ǣ�������
| A�� | ��-�ޣ�-1���ȣ�0��1�� | B�� | ��-1��0���ȣ�1��+�ޣ� | C�� | ��-1��0���ȣ�0��1�� | D�� | ��-�ޣ�-1���ȣ�1��+�ޣ� |
6����Բ$\frac{x^2}{16}+\frac{y^2}{12}=1$��������Ϊ��������
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{\sqrt{3}}{3}$ | D�� | $\frac{\sqrt{2}}{2}$ |
7����֪����Բ�ĽǵĻ�����Ϊ2���뾶Ϊ3cm�������ε����Ϊ��������
| A�� | 3cm2 | B�� | 6cm2 | C�� | 9cm2 | D�� | 18cm2 |
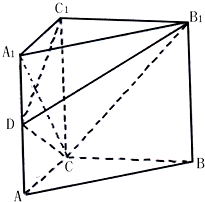 ij�Ҿ�װ����Ƶ���״����ͼ��ʾ��ֱ������ABC-A1B1C1�����У���ACB=90�㣬BCC1B1�DZ߳�Ϊ2����λ���ף��������Σ�AC=1����DΪ��AA1�ϵĶ��㣮
ij�Ҿ�װ����Ƶ���״����ͼ��ʾ��ֱ������ABC-A1B1C1�����У���ACB=90�㣬BCC1B1�DZ߳�Ϊ2����λ���ף��������Σ�AC=1����DΪ��AA1�ϵĶ��㣮