题目内容

对于函数f（x），若存在x0∈R，使f(x0)=x0成立，则称x0为f（x）的不动点，如果函数f(x)=ax2+bx+1(a＞0)有两个相异的不动点x1、x2.若x1＜1＜x2＜2,且f(x)的图象关于直线x=m对称，求证：＜m＜1.

思路解析：本题是不等式与二次函数的综合题，由题中“不动点”的特性——横、纵坐标相等，构造一个新的函数g(x)=f(x)-x=ax2+(b-1)x+1，使x1、x2为方程g(x)=0的两个“根”.然后根据二次函数的对称轴方程和根的判别式原理结合不等式性质证明结论.

证法一：设g(x)=f(x)-x=ax2+(b-1)x+1且a＞0，

∵x1＜1＜x2＜2,

∴(x1-1)(x2-1)＜0,

即x1x2＜(x1+x2)-1.

于是得x=m=-= (--)= (x1+x2)- x1x2

＞ (x1+x2)- ［(x1+x2)-1］

=.

又∵x1＜1＜x2＜2,

∴x1x2＞x1.

于是又有m= (x1+x2)- x1x2＜ (x1+x2)- x1=x2＜1.

故证得＜m＜1.

证法二：(1)设g(x)=f(x)-x=ax2+(b-1)x+1,且a＞0,

∴由条件x1＜1＜x2＜2,得g(1)＜0且g(2)＞0,

即

*

*

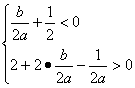
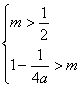
*m=-∈(,1).

练习册系列答案
相关题目
对于函数f（x），若存在区间M=[a，b]（其中a＜b），使得{y|y=f（x），x∈M}=M，则称区间M为函数f（x）的一个“稳定区间”．给出下列4个函数：
①f（x）=（x-1）2；②f（x）=|2x-1|；③f(x)=cos
π2
x；④f（x）=ex．其中存在“稳定区间”的函数有
 
（填出所有满足条件的函数序号）
对于函数f（x），若在其定义域内存在两个实数a，b（a＜b），使当x∈[a，b]时，f（x）的值域也是[a，b]，则称函数f（x）为“科比函数”．若函数f（x）=k+
x+2
是“科比函数”，则实数k的取值范围是
 
．
对于函数f（x），若存在x0∈R，使f（x0）=x0成立，则称x0为f（x）的不动点．如果函数
f（x）=ax2+bx+1（a＞0）有两个相异的不动点x1，x2．
（1）若x1＜1＜x2，且f（x）的图象关于直线x=m对称，求证：
12
＜m＜1；
（2）若|x1|＜2且|x1-x2|=2，求b的取值范围．
对于函数f（x），若f（x0）=x0，则称x0为f（x）的：“不动点”；若f[f（x0）]=x0，则称x0为f（x）的“稳定点”．函数f（x）的“不动点”和“稳定点”的集合分别记为A和B，即A={x|f[f（x）]=x}．
（1）设函数f（x）=ax2+bx+c（a≠0），且A=∅，求证：B=∅；
（2）设函数f（x）=3x+4，求集合A和B，并分析能否根据（1）（2）中的结论判断A=B恒成立？若能，请给出证明，若不能，请举以反例．
对于函数f（x），若存在x0∈R，使得f（x0）=x0，则称x0为函数f（x）的不动点．若函数f（x）=
x2+a
bx-c
（b，c∈N*）有且仅有两个不动点0和2，且f（-2）＜-
1
2
．
（1）试求函数f（x）的单调区间，
（2）已知各项不为0的数列{an}满足4Sn•f（
1
an
）=1，其中Sn表示数列{an}的前n项和，求证：(1-
1
an
)an+1＜
1
e
＜(1-
1
an
)an
（3）在（2）的前题条件下，设bn=-
1
an
，Tn表示数列{bn}的前n项和，求证：T2011-1＜ln2011＜T2010．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网