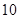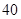题目内容
已知 表示等差数列
表示等差数列 的前
的前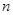 项和,且
项和,且 等于( )
等于( )
A. | B. | C. | D. |
A
解析试题分析:因为该数列是等差数列,所以 成等差数列,又因为
成等差数列,又因为 ,所以
,所以 ,所以
,所以 ,所以
,所以 ,所以
,所以 ,同理可求
,同理可求 ,所以
,所以
考点:本小题主要考查等差数列的性质的应用.
点评:等差数列、等比数列的性质可以简化运算,要灵活运用.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
等差数列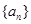 的前n项和为
的前n项和为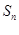 ,且
,且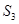 =6,
=6,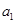 =4, 则公差d等于( )
=4, 则公差d等于( )
| A.1 | B.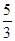 | C.- 2 | D.3 |
如图是从事网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推.若2013是第m行从左至右算的第n个数字,则(m,n)为( )
| A.(63,60) | B.(63,4) | C.(64,61) | D.(64,4) |
已知-1,a,b,-4成等差数列,-1,c,d, e,-4成等比数列,则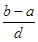 =( )
=( )
A.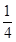 | B.-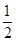 | C.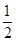 | D.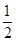 或- 或-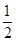 |
在等差数列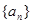 中,
中,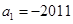 ,前n项和为
,前n项和为 ,且
,且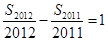 ,则
,则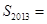
A.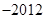 | B.2012 | C.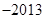 | D.2013 |
在等差数列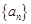 中,
中, ,则
,则 ( ).
( ).
| A.45 | B.75 | C.180 | D.300 |
在等差数列 等于 ( )
等于 ( )
| A.22 | B.18 | C.20 | D.13 |
已知 ,则数列
,则数列 是( )
是( )
| A.常数列 | B.摆动数列 | C.等差数列 | D.等比数列 |
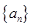 的前项和为
的前项和为 ,若
,若 三点共线,
三点共线, 为坐标原点,且
为坐标原点,且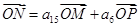 (直线
(直线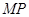 不过点
不过点 等于 ( )
等于 ( )